Konkaves Deltaeder
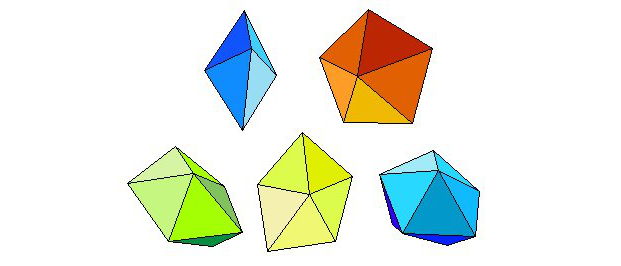
Können Sie aus 28 gleichen gleichseitigen Dreiecken ein Polyeder mit 16 Ecken und 42 Kanten und der Symmetrie des regulären Tetraeders bauen?
Ersetzen Sie die Flächen eines Tetraeders durch einander gleiche Anbauten.
Das Polyeder erhalten Sie, wenn Sie 4 reguläre Oktaeder an die Flächen des ebenfalls regulären Tetraeders fügen (und dabei zweimal vier Flächen einsparen).
Man kann dieses Polyeder auch als Tetraederstumpf ansehen, aus dem noch sechs Tetraeder herausgehackt worden sind.
An sich sind konkave Deltaeder (aus lauter gleichen gleichseitigen Dreiecken bestehende Polyeder) nichts besonders Seltenes, aber bei diesem Exemplar sind jeweils mehrere Kanten kollinear (d. h. fallen in gemeinsame Geraden) und jeweils mehrere Flächen komplanar (fallen also in gemeinsame Ebenen). Wie sieht es nun bei solcher Betrachtung mit der Bilanz der Ecken, Kanten und Flächen aus? Kanten und Ecken, die nur als Durchdringungsschnitte auftreten, werden dabei (wie bei den Sternpolyedern) nicht mitgezählt.
So gesehen, haben wir es mit 4 kleinen und 4 großen Dreiecken zu tun – letztere sind die vergrößerten Tetraederflächen – und parallel zu diesen mit 4 seltsam überschlagenen Sechsecken: Diese haben 6 Winkel von je 60o und abwechselnd kurze und lange Seiten. Das sind 12 Flächen. Als Ecken behalten wir nur die 12 äußeren, denn durch die inneren 4 laufen die 12 langen Kanten hindurch, und es enden keine in ihnen. Außer diesen 12 langen Kanten haben wir noch 12 kurze. Wir haben somit bei dieser Betrachtung (die sich an die bei Sternpolyedern übliche anlehnt) 12 Ecken, 24 Kanten und 12 Flächen. Das gibt erstaunlicherweise das topologische Geschlecht (Anzahl der Löcher) \(g= 1\), obwohl das Polyeder einen ganz gewöhnlichen zusammenhängenden Innenraum hat und keineswegs die Topologie des Torus aufweist. Der Grund dafür ist, dass wir die großen Dreiecke als sich durchdringende Flächen um das innere Tetraeder herum ansehen.
Wenn wir von der Regularität dieses Tetraeders und/oder der der angebauten Oktaeder absehen, bestehen Kollinearität und Komplanarität nicht mehr, und wir haben nur noch die Betrachtung vom Beginn der Aufgabe zur Wahl, und dort war das Geschlecht \(g=0\), denn wir haben dabei 16 Ecken, 42 Kanten und 28 Flächen, und die Euler-Charakteristik \(\chi\) (Ecken – Kanten + Flächen) ist ganz normal \(\chi=2-2g=16 – 42 + 28 = 2\) und entspricht der einer Kugeloberfläche.
Schreiben Sie uns!
Beitrag schreiben