Überlappende Quadranten
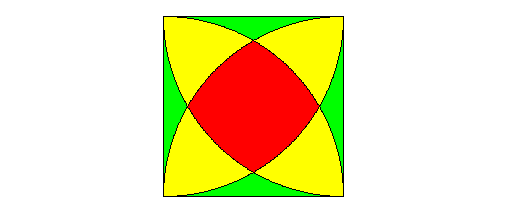
Wie teilt sich die Fläche dieses Quadrates auf die drei Farben auf?
Teilen Sie das Quadrat in Dreiecke und Kreissektoren auf.
Nennen wir die Seitenlänge des Quadrats \(a\); dann ist die Gesamtfläche \(A_{\rm ges}=a^2\).
Dieses Quadrat ist durch Viertelkreise zerteilt. Die Fläche der Sektoren \(B\) beträgt jeweils ein Drittel des Viertelkreises und somit 1/12 eines vollen Kreises mit Radius \(a\): \(A_B=\frac{1}{12}\pi a^2\).
Das hellblaue Dreieck \(C\) ist gleichseitig (alle Seiten sind gleich dem Kreisradius \(a\)), also ist seine Höhe \(h_C=a \frac{\sqrt{3}}{2}\) und seine Fläche \(A_C=a^2 \frac{\sqrt{3}}{4}\).
Damit ist die Fläche eines kleinen grünen Zwickels \(G\) gleich der Gesamtfläche minus zwei Kreissektoren \(B\) minus ein Dreieck \(C\): \(A_G=A_{\rm ges}-2A_B-A_C = a^2 – \frac{1}{6}\pi a^2 -a^2\frac{\sqrt{3}}{4}\).
Als nächsten Schritt berechnen wir den Flächeninhalt des "gotischen Spitzbogens" \(F\), der aus einem hellblauen Dreieck \(C\) und zwei violetten Kreissegmenten \(V\) besteht. Da wir die Fläche von \(V\) nicht kennen, dafür aber die Fläche von \(C\) und \(V\) zusammen (genau ein Sechstel des Flächeninhalts des Kreises mit Radius \(a\)), berechnen wir die Fläche von \(F\) über einen kleinen Umweg: \(A_F=2 A_{C \cup V}-A_C = \frac{1}{3}\pi a^2 – a^2 \frac{\sqrt{3}}{4}\).
Zum Ziel kommen wir nun mit zwei Exemplaren von \(F\): Eines steht wie eingezeichnet auf dem Boden, das andere hängt von der Oberseite des Quadrats herab. Beide zusammen überdecken das ganze Quadrat bis auf die zwei Zwickel \(G\) links und rechts. Die Fläche \(R\) wird doppelt überdeckt. Daraus ergibt sich \(2A_F=A_{\rm ges}+A_R-2A_G\). Diese Gleichung können wir nach der (einzigen) Unbekannten \(A_R\) auflösen: \(A_R=2(A_F+A_G)-A_{\rm ges} = a^2+\frac{1}{3} \pi a^2-a^2\sqrt{3} \).
Den Inhalt der letzten unbekannten Fläche \(Y\) finden wir, indem wir feststellen, dass der Spitzbogen \(F\) aus einem \(G\), einem \(R\) und zwei Stück \(Y\) besteht: \( A_Y=\frac{1}{2}(A_F-A_G-A_R) = \frac{1}{12}\pi a^2-a^2+a^2\frac{\sqrt{3}}{2}\).
Ausgerechnet: \(A_R \approx 0{,}3151 a^2, A_G \approx 0{,}04339 a^2, A_Y \approx 0{,}1278 a^2\).
Schreiben Sie uns!
Beitrag schreiben