Verliebte Wanzen

An den Ecken eines regulären Vielecks befindet sich je eine Wanze, aber es kommt noch unrealistischer: Sie ist verliebt in die im Gegenuhrzeigersinn nächste (Varianten: übernächste, über-über-nächste usw.). Alle marschieren nun gleichzeitig los, mit gleicher Geschwindigkeit, und sie halten immer Kurs genau auf den jeweiligen Liebling.
Infolgedessen schrumpft und dreht sich das Vieleck bzw. Sternpolygon, bleibt aber regulär, bis sich alle Wanzen im Mittelpunkt treffen. Wie weit ist dann jede gelaufen? Besonders einfach ist es für das Quadrat und noch ziemlich einfach für Dreieck und Sechseck.
Bleiben wir zuerst bei 4 Wanzen, also beim schrumpfenden Quadrat: Wie ändert sich ihr Abstand, wenn jede einen (sozusagen sehr kleinen) Schritt auf ein Ziel zu macht, das (hinreichend langsam) genau seitwärts wandert?
Der Abstand verkleinert sich ziemlich genau um die Schrittlänge der Wanze, sogar ganz genau, wenn wir den Grenzfall mit verschwindend kurzen Schritten betrachten. Der Weg jeder Wanze bis zum gemeinsamen Treffpunkt ist also so lang wie die ursprüngliche Quadratseite.
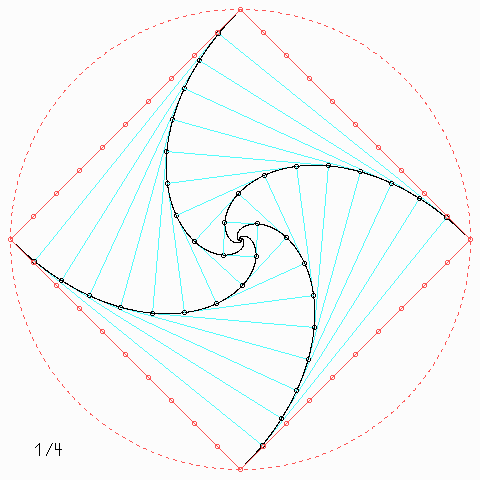
Für andere Zahlen sehen die Figuren so aus:
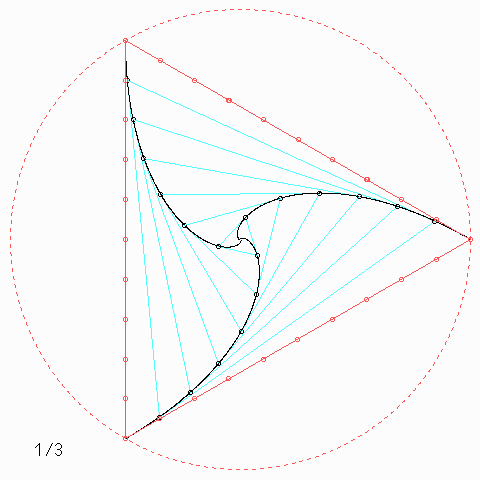
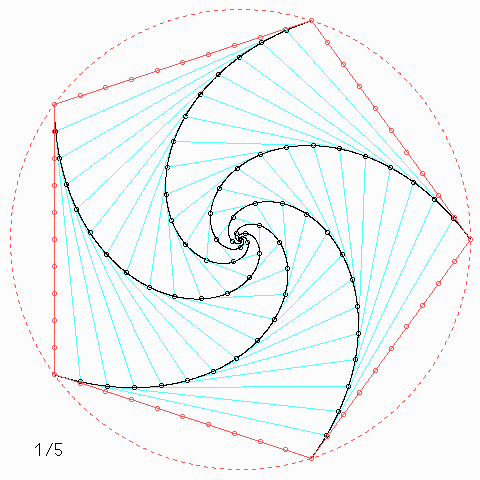
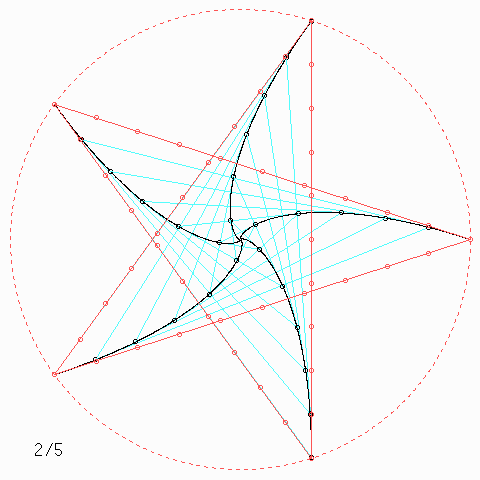
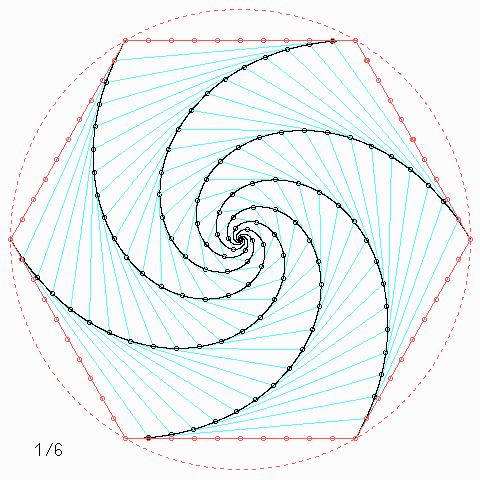
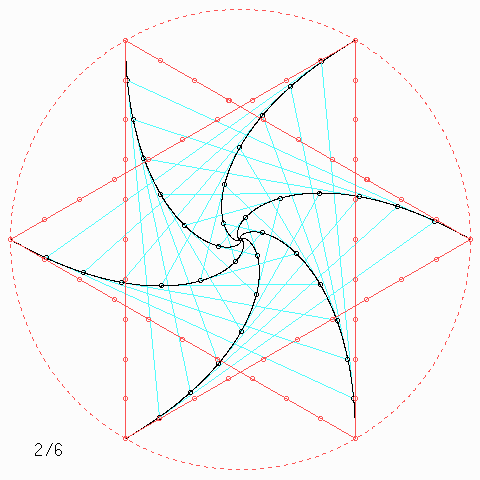

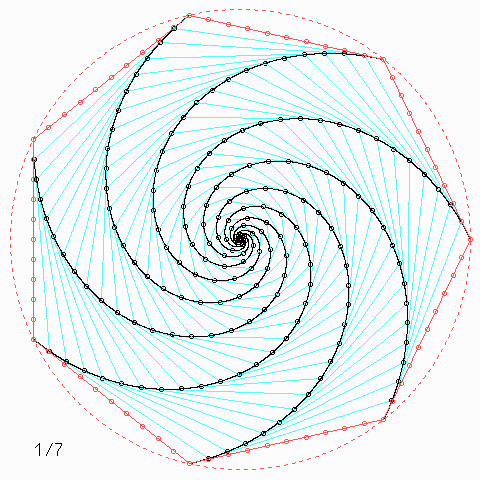
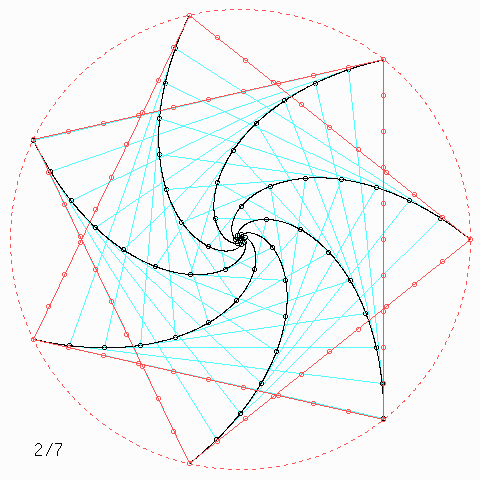
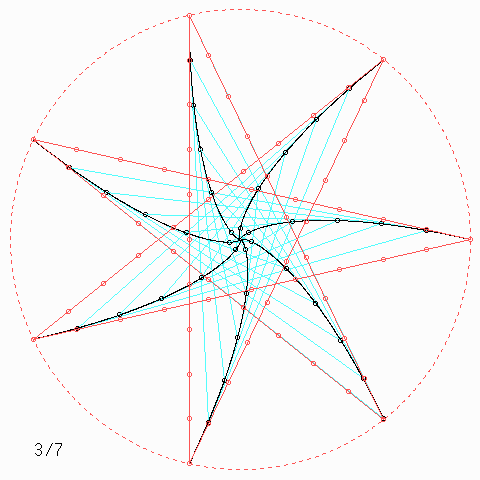
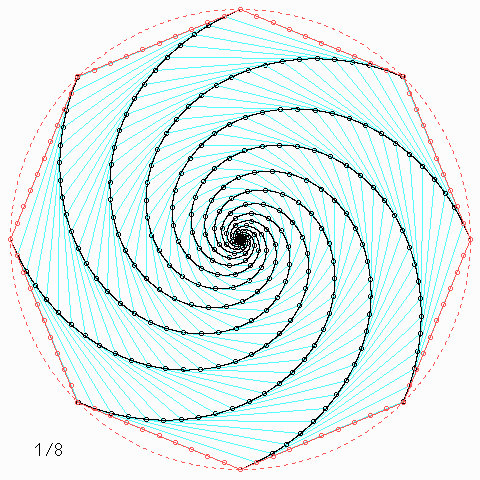
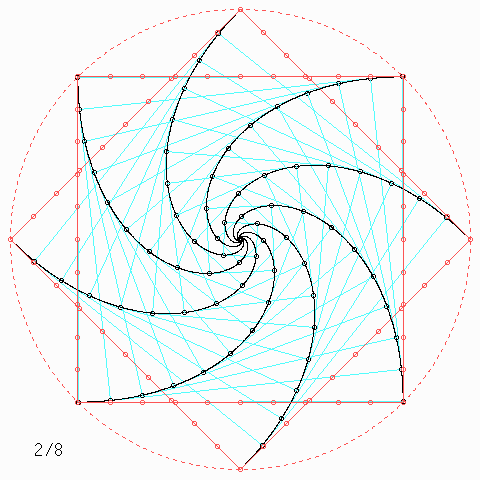
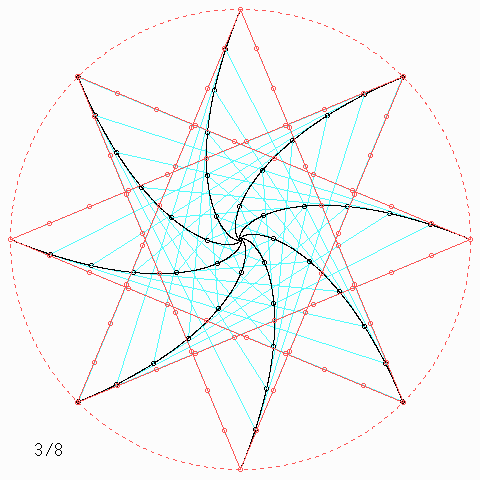
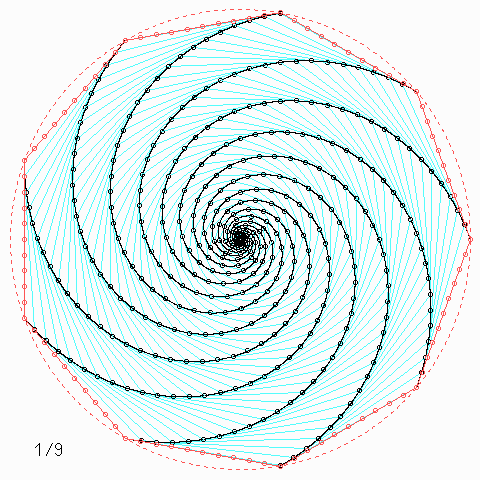
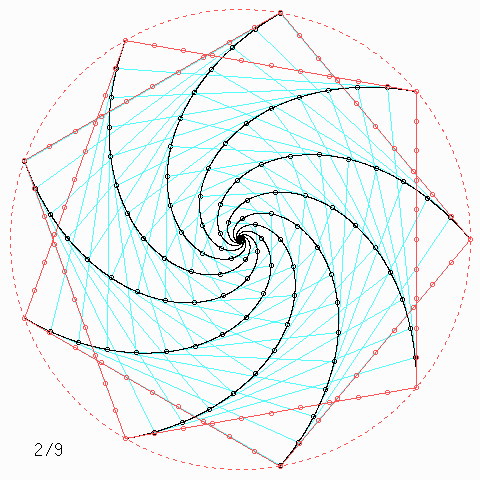
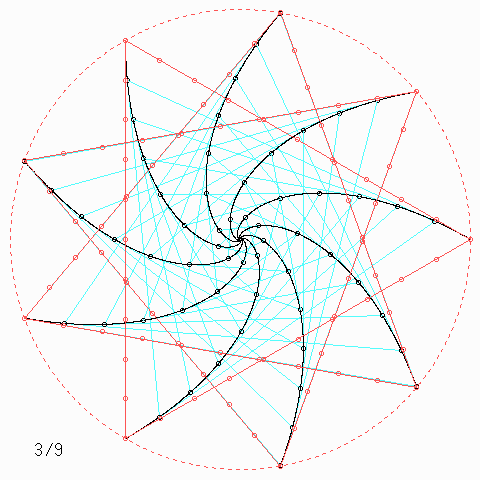
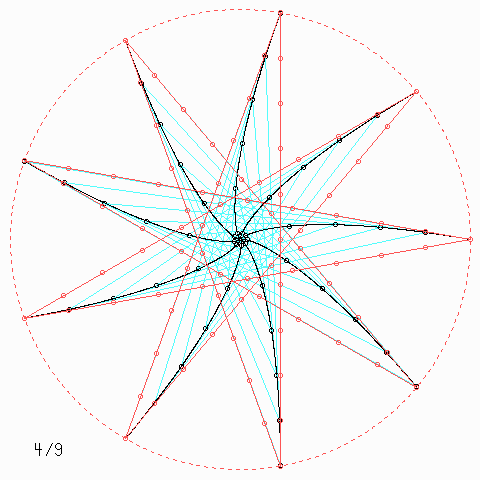
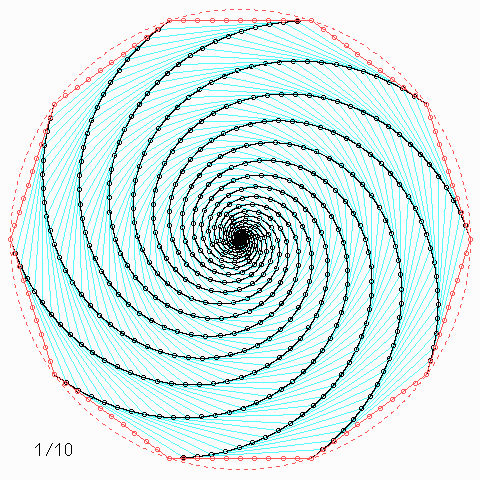
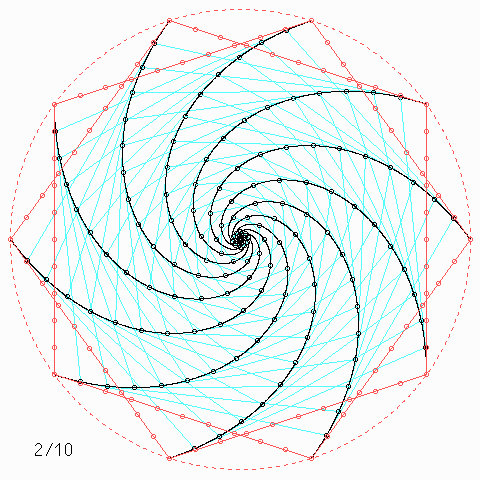
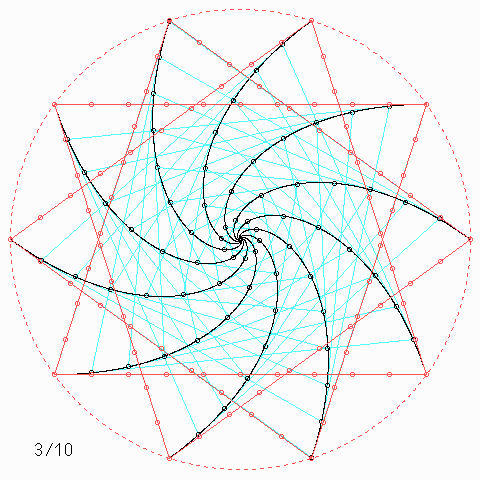
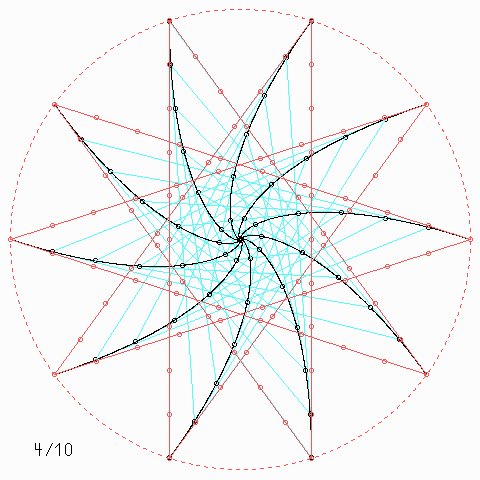
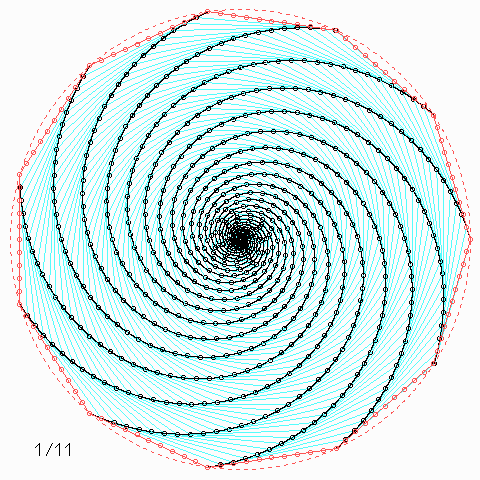

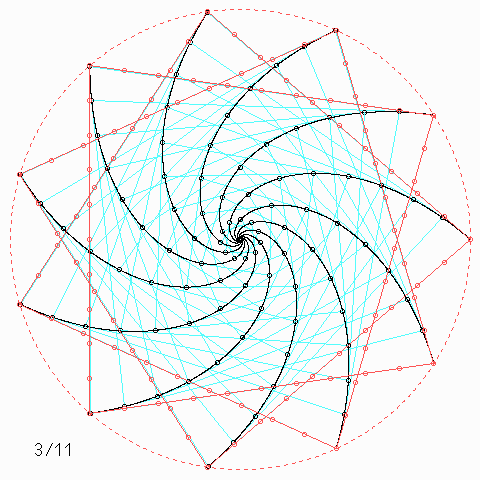
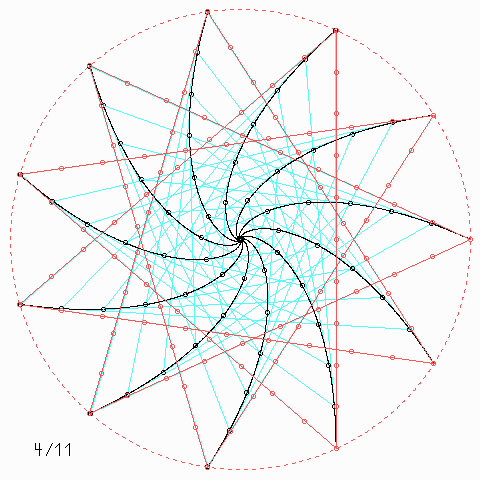
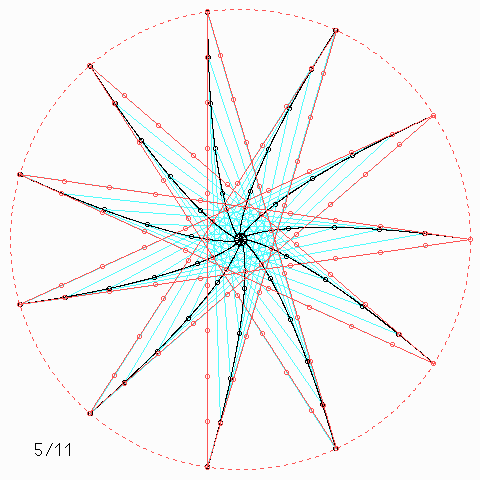
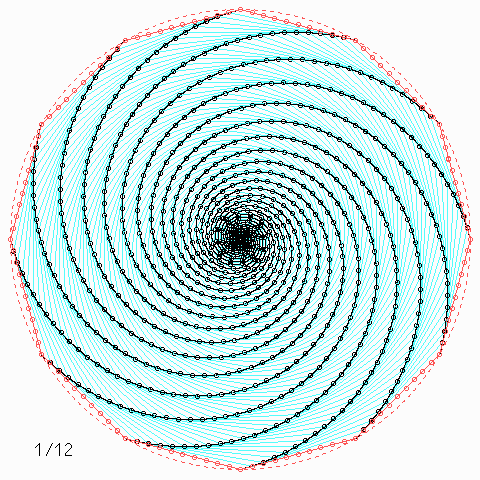
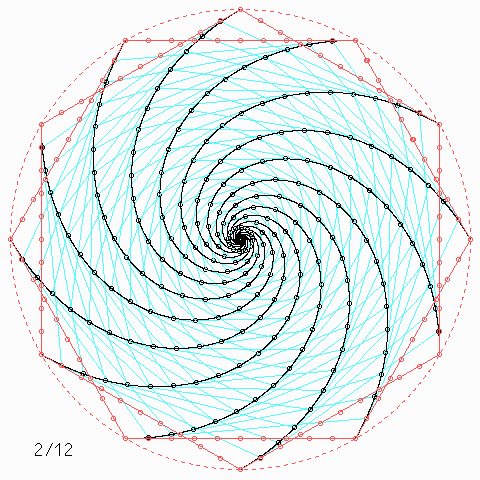
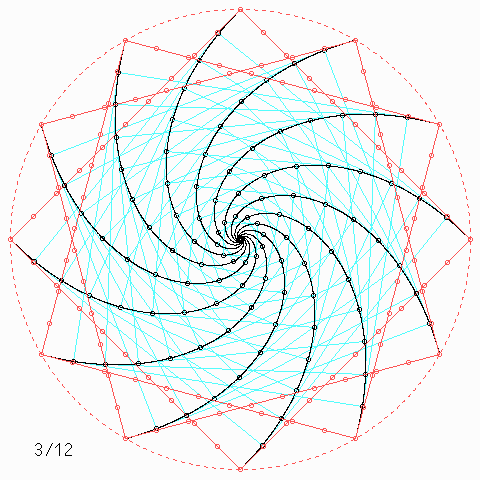
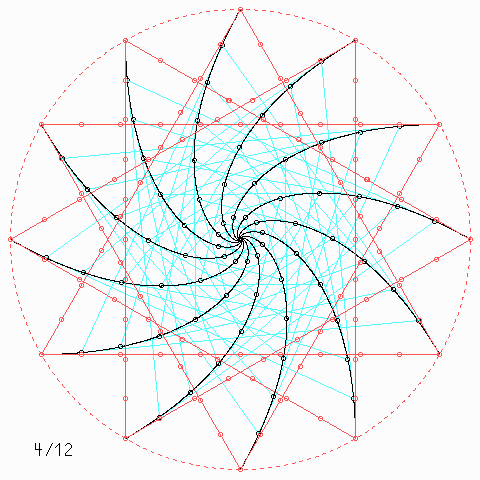
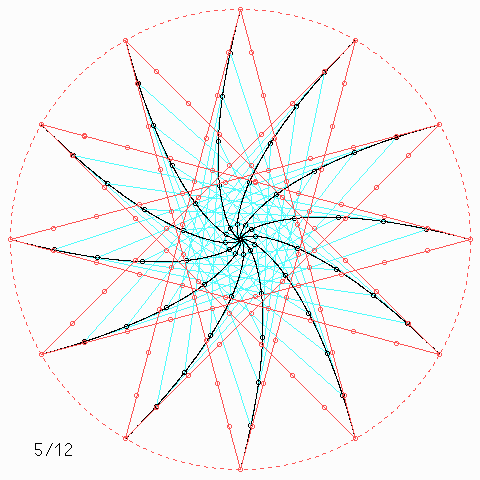
Welche Symmetrie-Eigenschaft hat jede einzelne der \(n\) Kurven, auch wenn \(n\) nicht unbedingt 4 ist, und wie kann man daraus etwas über die Kurvenlänge herausfinden?
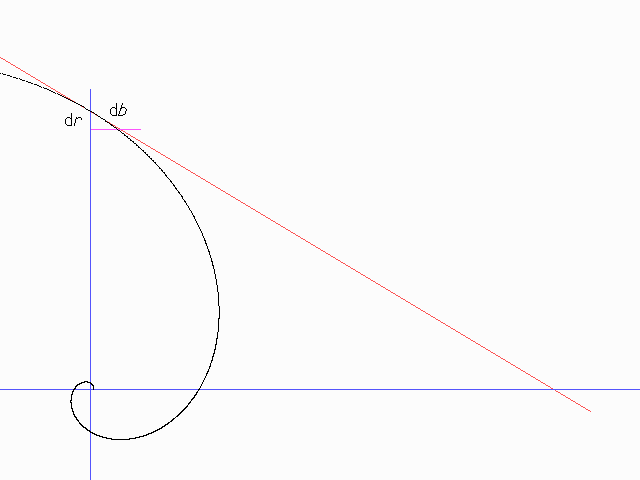
Die schrumpfenden Polygone oder Sternpolygone machen Drehstreckungen um den gemeinsamen Mittelpunkt. Für die Verbindungsstrecke zwischen einer Ecke und diesem Mittelpunkt hat sich die (etwas gewöhnungsbedürftige) Bezeichnung "Radius" eingebürgert. Jede Ecke wandert zu jedem Zeitpunkt in eine Richtung, die mit dem jeweils aktuellen Radius stets denselben Winkel (den "Tangentenwinkel") bildet. Beim Quadrat ist dieser Winkel 45o, allgemein ist er die Hälfte des Innenwinkels des Polygons. Die Kurven sind also (abgesehen von der Position des Mittelpunktes und der Orientierung) allein durch diesen Winkel gekennzeichnet. Eine Vergrößerung wird sozusagen durch eine passende Drehung ausgeglichen, aber derartige ("logarithmische") Spiralen mit verschiedenen Winkeln sind nicht deckungsgleich.
Betrachten wir nun ein kleines Wegstück auf der Kurve, das im Bild noch viel zu groß gezeichnet ist. Zu ihm gehört eine Änderung des Radius, und wegen der Ähnlichkeit der beiden rechtwinkligen Dreiecke verhalten sie sich wie der Tangentenabschnitt vom Kurvenpunkt bis zum (hier waagerecht liegenden) Lot zum Radius zu der Länge \(r\) des Radius. Insgesamt ist die (verbleibende) Weglänge der Wanze gleich der Länge dieses Tangentenabschnitts, und die beträgt \(r / \sin \alpha\), wobei \(\alpha\) der Tangentenwinkel ist. Das ist eine erstaunlich einfache und einfach einzusehende Eigenschaft der Kurvenlänge der logarithmischen Spirale. Für ein reguläres \(n\)-Eck mit der Seitenlänge 1 ergibt sich die Gesamtlänge eines Wanzenwegs zu \(s=1/(2 \sin \alpha) = 1/\sin(2\pi/n))\).
Was gibt es, wenn man eine logarithmische Spirale so aus ihrer Ebene herauszieht, dass der Abstand jedes ihrer Punkte von dieser Ebene proportional zu dessen Winkelkoordinate ist?
Die räumliche Kurve hat als Parallelprojektionen (Schattenwürfe mit unendlich ferner Lichtquelle) natürlich in einer Ebene die bisher betrachtete logarithmische Spirale, in zwei zu dieser und zueinander rechtwinkligen Ebenen abklingende Sinus- bzw. Kosinus-Kurven:
Mit veränderlichem Schnittwinkel sieht das dann so aus:
Der Grenzfall mit 90o ist natürlich die Wendel (Schraubenlinie) mit Kreis und nicht-abklingenden Kurven als Projektionen.



Schreiben Sie uns!
Beitrag schreiben