Waterhouse
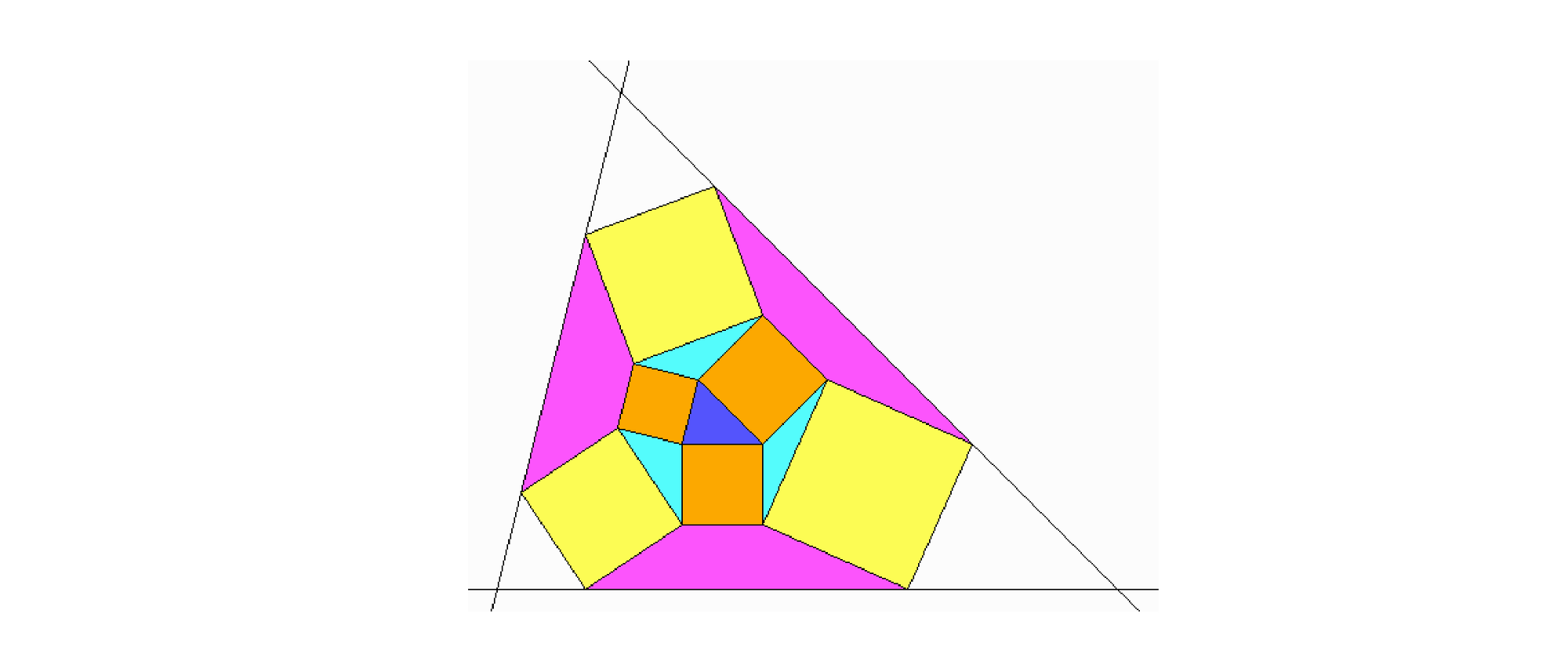
An das blaue Dreieck in der Mitte werden außen drei orangefarbene Quadrate mit den jeweiligen Seitenlängen angefügt. Durch hell-cyanfarbene Dreiecke wird die konkave neuneckige Figur zu einem konvexen Sechseck ergänzt. An dessen neue Seiten werden nun die gelben Quadrate angefügt und durch die purpurnen Vierecke konvex ergänzt, und deren äußere Seiten werden zu einem großen Dreieck verlängert. Was kann man über dieses Dreieck und über die Flächen der drei purpurnen Vierecke sagen?
Suchen Sie nach Dreiecken, die zum zentralen blauen Ausgangsdreieck flächengleich oder auch deckungsgleich sind.
Verdoppelt man die hellblauen Dreiecke zu Parallelogrammen, so sieht man sogleich, dass diese jeweils aus zwei zum Ausgangsdreieck deckungsgleichen Dreiecken bestehen.
Es sind also die vier hellblauen Dreiecke zwischen den orangefarbenen Quadraten untereinander sowie zum Urdreieck flächengleich. Nun baut man mehrere Exemplare des Urdreiecks (dunkelblau) und seiner flächengleichen Kollegen (grünblau) an die Figur an.
Die jetzt schraffierten Vierecke bestehen aus je 5 Dreiecken, von denen 3 zum Ausgangsdreieck deckungsgleich, aber alle 5 zu ihm flächengleich sind.
Anhand der Winkelbilanzen findet man, dass es sich um Trapeze handelt. Wegen der Trapezeigenschaften ist das ganz große Dreieck zum Ausgangsdreieck ähnlich und parallel ausgerichtet. Im Falle des gleichschenklig-rechtwinkligen Dreiecks kann man sogar bestimmen, um welchen Faktor es größer ist: 8 für die Längen, also 64 für die Fläche.
Das war's
Mit diesem Rätsel ist der bunte und reichhaltige Vorrat, den uns Norbert Treitz hinterlassen hat, erschöpft. Der bearbeitende Redakteur verabschiedet sich nicht ohne eine gewisse Wehmut von dem Projekt und seinen treuen Lesern, die oft genug zu Klar- (und gelegentlich zu Richtig-)stellungen beigetragen haben.
Christoph Pöppe
Schreiben Sie uns!
Beitrag schreiben