Hemmes mathematische Rätsel: Welche Figur ist gesucht?

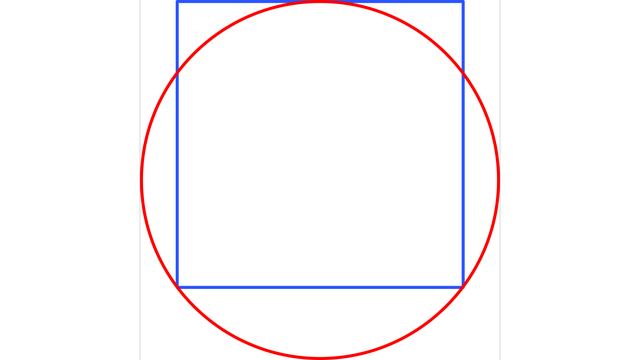
Der Inkreis eines Quadrats hat eine interessante Eigenschaft. Dreht man ihn stetig um 360 Grad, also einmal »im Kreis«, berührt er während der gesamten Drehung immer alle vier Seiten des Quadrats.
Gibt es noch eine andere ebene Figur, die man in ein Quadrat setzen kann und die bei einer Drehung um 360 Grad stets alle vier Seiten des Quadrats berührt, sie aber nie schneidet?
Wenn nein, warum nicht? Der Drehpunkt der Figur braucht dabei übrigens nicht der Mittelpunkt des Quadrats zu sein. Er darf sogar bei der Drehung seine Lage im Quadrat verändern.
Die Dicke einer geometrischen Figur ist der Abstand zweier paralleler Geraden, die man links und rechts an die Figur zeichnet. Normalerweise ist die Dicke einer Figur nicht konstant, denn wenn man diese dreht, kann der Abstand der beiden Parallelen größer oder kleiner werden. Die Dicke eines Quadrates der Seitenlänge 1 beispielsweise kann jeden Wert zwischen 1 und √2 annehmen.
Figuren, die, egal wie man sie dreht, immer die gleiche Dicke haben, nennt man Gleichdicke. Das bekannteste Gleichdick ist der Kreis, aber es gibt auch noch beliebig viele andere. Das einfachste davon ist das Reuleauxsche Dreieck. Es entsteht, wenn man bei einem gleichseitigen Dreieck über jede Seite einen Kreisbogen schlägt, der die jeweils gegenüberliegende Ecke als Mittelpunkt hat. Dieses Bogendreieck ist überall eine Dreiecksseitenlänge dick.
Legt man nicht nur links und rechts Geraden an ein Gleichdick, sondern auch oben und unten, so bilden diese Geraden ein Quadrat, das das Gleichdick umschließt. Ganz egal, um welchen Winkel man das Gleichdick in dem Quadrat dreht, es passt stets genau hinein und berührt alle vier Seiten. Allerdings muss dabei, außer beim Kreis, auch gleichzeitig sein Mittelpunkt immer etwas verschoben werden.




Schreiben Sie uns!
Beitrag schreiben