Hemmes mathematische Rätsel: Welches Dreieck ist am größten?
Walther Lietzmann (1880–1959) war einer der bedeutendsten Mathematikdidaktiker Deutschlands. Sein Buch »Der Pythagoreische Lehrsatz« erschien zwischen 1912 und 1966 in zahlreichen Auflagen. Daraus stammt die folgende Aufgabe:
Um den Satz des Pythagoras graphisch darzustellen, zeichnet man üblicherweise Quadrate an die beiden Katheten und an die Hypotenuse eines rechtwinkligen Dreiecks. Der Flächeninhalt des Hypotenusenquadrates ist dann genauso groß wie der der beiden Kathetenquadrate.
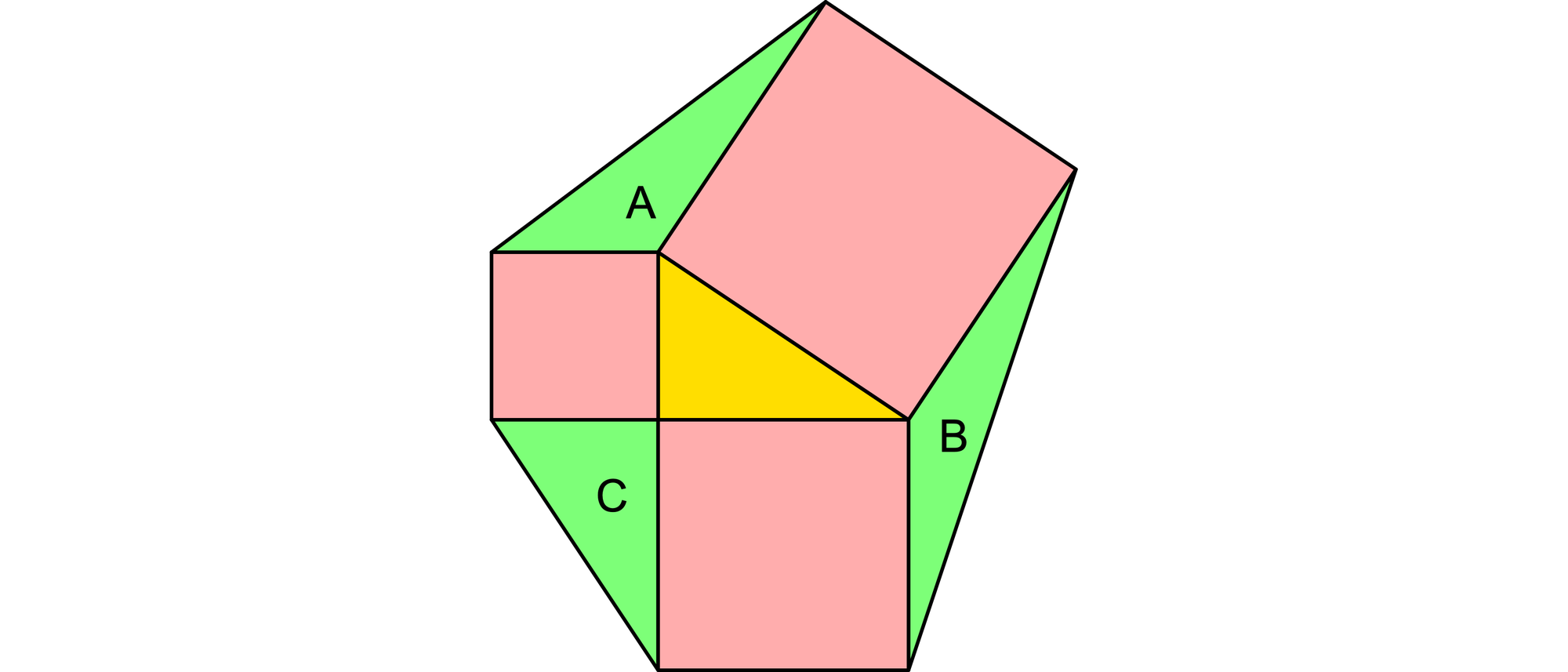
Die Zeichnung wird nun um drei zusätzliche Dreiecke A, B und C erweitert. Welches dieser Dreiecke hat den größten Flächeninhalt?
Zeichnet man das ursprüngliche rechtwinklige gelbe Dreieck mit den Kathetenlängen a und b auf alle vier Seiten des Hypotenusenquadrats, wird dieses anschließend von einem rotumrandeten Quadrat der Seitenlänge a + b umschlossen. Nun erkennt man die Lösung leicht.
Das ursprüngliche gelbe Dreieck, das grüne Dreieck A und das grüne Dreieck C haben jeweils eine Grundseite a und eine Höhe b, und das grüne Dreieck B hat eine Grundseite b und eine Höhe a. Folglich haben alle vier Dreiecke den gleichen Flächeninhalt von ab/2.






Schreiben Sie uns!
Beitrag schreiben