Hemmes mathematische Rätsel: Wie groß ist das Volumen?
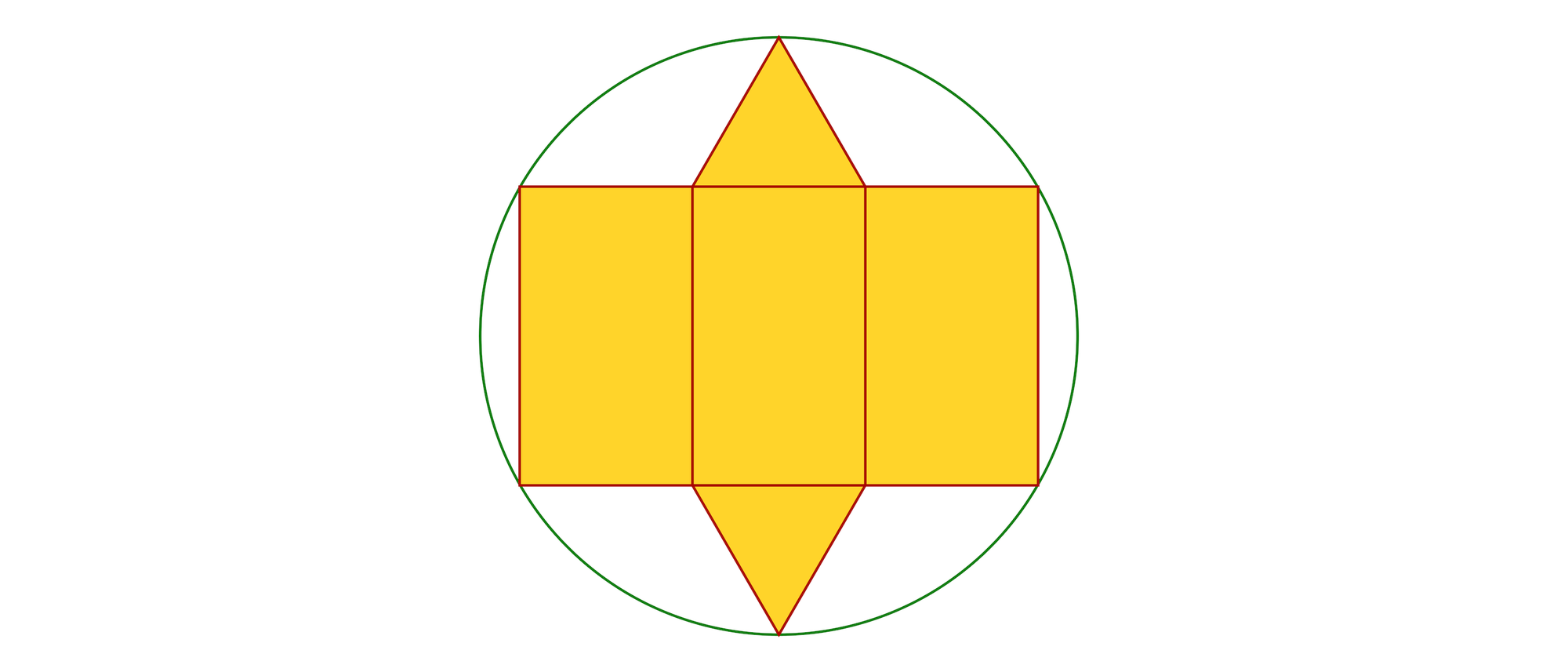
Das heutige Rätsel stammt von dem 1951 geborenen Architekten Karl Flormann aus Bielefeld. Ein regelmäßiges Dreiecksprisma hat je ein gleichseitiges Dreieck als Grund- und als Deckfläche und drei Rechtecke als Seitenflächen. Das Bild zeigt ein Netz eines regelmäßigen Dreiecksprismas. Seine sechs äußeren Ecken liegen dabei auf dem Umfang eines Kreises, der den Radius 1 hat. Wie groß ist das Volumen des Prismas?
Damit die sechs äußeren Eckpunkte des Prismanetzes auf dem Kreisumfang liegen, müssen sie alle vom Mittelpunkt M gleich weit entfernt sein. Das Dreieck AGI ist gleichseitig. Folglich ist der Winkel HAI 30° und der Winkel AIH 60° groß. Das Dreieck AIF ist gleichschenklig. Sein stumpfer Winkel ist 120° groß, und damit sind seine beiden spitzen Winkel 30° groß. Daraus folgt, dass das blaue Dreieck AMF gleichseitig ist und die Seitenlänge 1 hat. Dies gilt wegen der Symmetrie auch für die Dreiecke AMB, CMD und DME. Daraus ergibt sich, dass auch die Dreiecke BMC und EMC gleichseitig sein müssen und ABCDEF ein regelmäßiges Sechseck der Seitenlänge 1 ist. Die Grundfläche AGI des Prismas hat die Höhe AH = 1/2 und damit nach dem Satz des Pythagoras die Seitenlänge GI = 1/3√3. Ihr Flächeninhalt beträgt folglich 1/2 · 1/2 · 1/3√3 = (√3)/12. Hieraus ergibt sich mit der Höhe BC = 1 für das Prisma ein Volumen von 1 · (√3)/12 ≈ 0,144.
Schreiben Sie uns!
Beitrag schreiben