Hemmes mathematische Rätsel: Wie lang ist die Strecke?
© Heinrich Hemme (Ausschnitt)
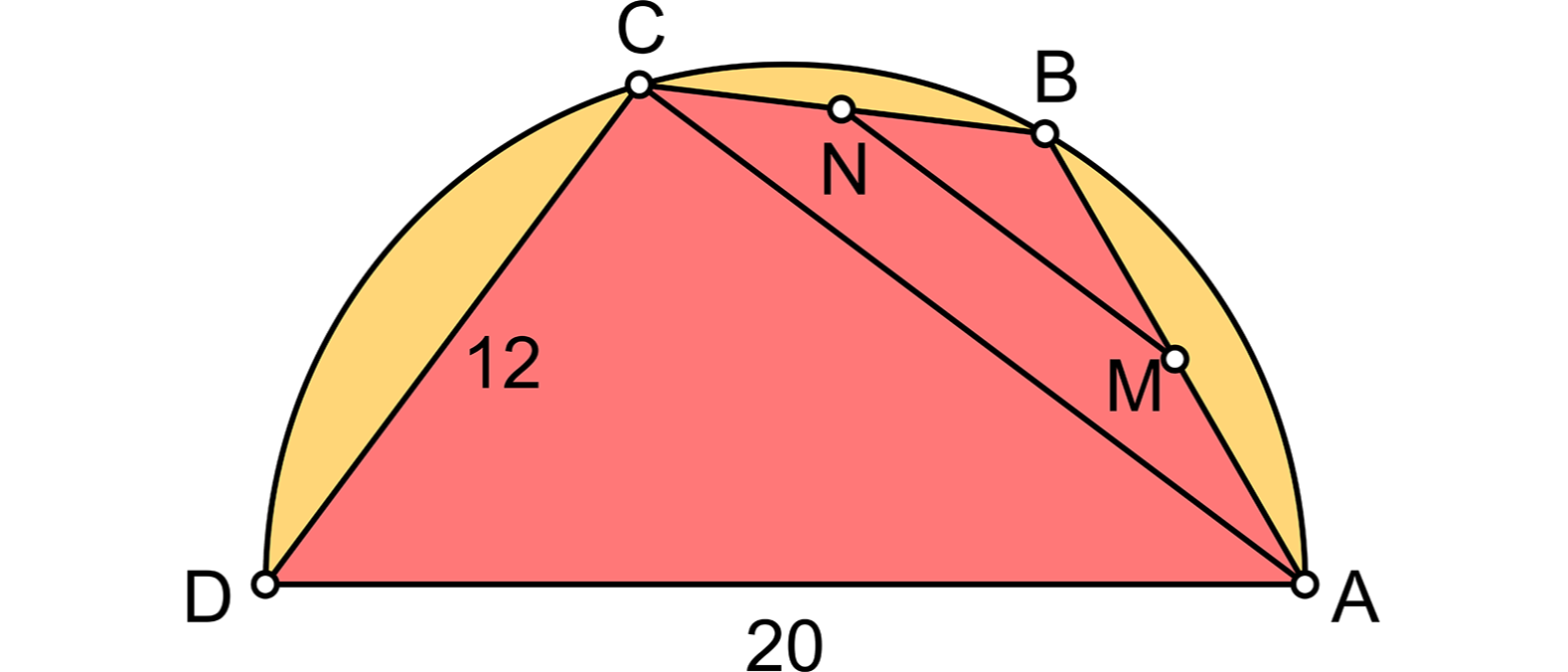
In einem Halbkreis mit dem Radius 10 bilden der Durchmesser AD und die drei Sehnen AB, BC und CD ein unregelmäßiges Viereck. Die Sehne AB hat die Länge 10 und die Sehne CD die Länge 12. Die Strecke MN verbindet die Mittelpunkte der Sehnen AB und BC. Wie lang ist sie?
Nach dem Satz des Thales ist das Dreieck ACD rechtwinklig. Somit hat die Seite AC die Länge √(202 – 122) = 16. Die Punkte M und N halbieren die Seiten AB und BC des Dreiecks ABC. Folglich liegt die Strecke MN parallel zur Dreiecksseite AC und ist nach dem Strahlensatz halb so lang wie diese und hat also die Länge 8. Die Länge der Sehne AB spielt dabei keine Rolle.
© Heinrich Hemme (Ausschnitt)
Schreiben Sie uns!
Beitrag schreiben