Kürzlich hatte ich Glück. Es gab keine Weihnachtskekse mehr und die von den Feiertagen übrig gebliebene Schokolade war ebenfalls schon aufgegessen. Doch in der hinteren Ecke eines Küchenschranks habe ich noch eine Packung bunter Schokolinsen gefunden. Der erste Griff in die Tüte lieferte eine grüne, zwei rote und sieben blaue Süßigkeiten. Eigentlich war mir das egal, denn der Farbstoff ist geschmacklos. Trotzdem habe ich mich über die blaue Übermacht in meiner Stichprobe gewundert und mich gefragt, wie wahrscheinlich so ein Ereignis ist. Gut, ich hätte einfach die Tüte ausleeren und nachzählen können. Aber man kann dafür auch diese Formel verwenden:

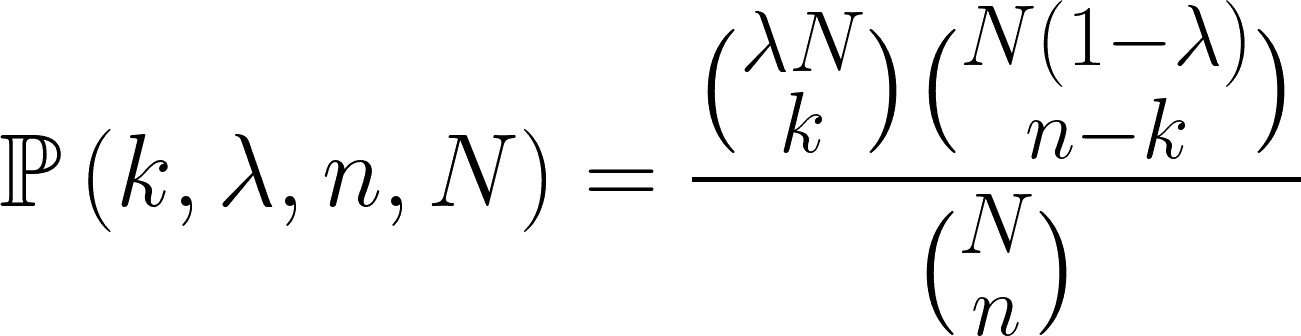
In unserem Beispiel wird in dieser Formel die Gesamtzahl der Schokolinsen in der Packung mit N bezeichnet. Der Anteil der blauen Linsen an der Gesamtzahl wird mit λ beschrieben, die Anzahl der bei der Stichprobe herausgegriffenen Linsen mit n und die darin gefundenen blauen Exemplare mit k. Setzt man die entsprechenden Werte ein, dann ergibt sich daraus die Wahrscheinlichkeit ℙ, dass man unter den n Linsen genau k blaue findet.

Das Problem daran: Der Anteil der blauen Linsen λ ist unbekannt, allerdings interessiert mich genau dieser Wert. Das macht aber nichts, denn dafür kann man die »Maximum-Likelihood-Methode« verwenden. Vereinfacht gesagt probiert man dabei verschiedene Werte für λ aus (bei einem fixen Wert für N) und sieht nach, wann die Wahrscheinlichkeit, unter n Linsen genau k mit der Farbe blau zu finden, maximal wird.

Von Schokolinsen zu deutschen Panzern

Im Fall der Schokolinsen hätte ich natürlich wirklich einfach alle nach Farben sortieren und zählen können – so groß war die Tüte auch wieder nicht. Doch es gibt durchaus Situationen, in denen man auf Schätzungen angewiesen ist. Ein historisch interessantes Beispiel ist das »German tank problem« beziehungsweise das »Problem der deutschen Panzer«. Im Zweiten Weltkrieg wollten die Alliierten wissen, wie gut Deutschland darin ist, Panzer zu bauen. Diese Information hatten sie natürlich nicht, dafür aber zumindest ein paar erbeutete Panzer. Die dort verwendeten Bauteile hatten Seriennummern, und mit denen war es möglich, eine Schätzung über die Gesamtzahl der produzierten Teile zu erhalten. Hat man etwa vier Panzer mit den Seriennummern 20, 31, 44 und 61, kann man eine entsprechende mathematische Schätzung durchführen: Bei welcher Gesamtzahl an Panzern ist es am wahrscheinlichsten, bei einer Stichprobe von vier Stück keine Seriennummer größer als 61 zu erhalten?

In der Realität war die Sache natürlich komplexer; unterschiedliche Bauteile der Panzer hatten unterschiedliche Seriennummern; es gab verschiedene Modelle, die nicht alle fortlaufend nummeriert wurden, und so weiter. Am Ende waren die mathematischen Schätzungen jedoch überraschend gut. Schätzmethoden wie das Maximum-Likelihood-Prinzip werden nicht nur für Geheimdienstoperationen im Krieg verwendet. Man benutzt sie in der Biologie, um Verwandtschaftsbeziehungen zwischen Lebewesen zu bestimmen, bei Datenanalysen und Vorhersagen in Sozial- und Wirtschaftswissenschaft oder bei Algorithmen zum Maschinenlernen.

Bei meinen Schokolinsen habe ich am Ende auf eine Maximum-Likelihood-Schätzung verzichtet und sie einfach alle aufgegessen. Die Farbe hat ja keinen Einfluss auf den Geschmack – ganz anders als bei Gummibärchen, wo es definitiv eine Farbe gibt, die besser als anderen schmeckt (die weißen). Keine noch so komplexe Formel wird mich vom Gegenteil überzeugen können.