Bosonensterne (engl. boson stars, BS) sind kompakte Objekte, die nur aus Skalarfeldern (siehe skalare Bosonen) zusammengesetzt sind. Salopp könnte man von Bosonenbällen sprechen. In der theoretischen Astrophysik werden Modelle solcher Sterne (die durchaus viel schwerer als massereiche Sterne werden können) diskutiert. Eventuell könnten Bosonensterne als Alternative zu Schwarzen Löchern existieren. Astronomen sind daran interessiert, das Wesen der kompakten Objekte auf der Grundlage von Beobachtungen zu entschlüsseln. Sie wollen herausfinden, ob es beispielsweise ein Weißer Zwerg, ein Neutronenstern, ein Schwarzes Loch oder ein Bosonenstern ist, was sie da beobachten. Daher ist die Physik der Bosonensterne nach wie vor ein aktuelles Forschungsfeld.
Die grundsätzliche Idee ist, physikalische Modelle von Bosonensternen zu entwickeln, daraus Vorhersagen über Masse oder Radius beispielsweise zu machen und diese Prognosen an der astronomischen Beobachtung zu testen. Falls alles passt, wäre die Existenz von Bosonensternen nicht auszuschließen.

Physik im Bosonenstern

Die Skalarfelder im Bosonenstern können miteinander wechselwirken oder wechselwirkungsfrei behandelt werden; sie können auch komplexwertig oder reell sein – daraus resultieren unterschiedliche Eigenschaften der Bosonensterne. Im Prinzip bestehen Bosonensterne aus Bose-Einstein-Kondensaten. Zur Beschreibung dieser Objekte muss die Quantentheorie verwendet werden. Genauer gesagt spielt die Quantenstatistik eine Rolle, die sich zur Beschreibung so genannter Bosegase eignet.
Die Theorie skalarer Felder involviert als Bewegungsgleichung des Feldes die Klein-Gordon-Gleichung; koppelt man diese nun an die Einsteinschen Feldgleichungen der Allgemeinen Relativitätstheorie so resultiert ein Gleichungssystem mit der Bezeichnung Einstein-Klein-Gordon-Gleichungen, die die Dynamik von Bosonensternen relativistisch und feldtheoretisch beschreibt.
Es gibt in der Literatur auch nicht-relativistische Zugänge, die Bosonenphysik und Newtonsche Gravitation nutzen.

Entstehung

Die Theorie skalarer Felder wird intensiv in der modernen Kosmologie ausgenutzt (siehe z.B. Inflaton, Cosmon, Radion). Skalarfelder gibt es tatsächlich in der Natur, so dass der Gravitationskollaps einer Bosonenwolke zu einem Bosonenstern plausibel erscheint. Als Entstehungskriterium kann trotz Quanteneffekte das klassische Jeans-Kriterium verwendet werden. Ein kugelsymmetrischer Bosonenstern kann sich durch einen dissipationsfreien Prozess bilden, der Gravitationskühlung (engl. gravitational cooling) getauft wurde (Seidel & Suen 1994). Der Prozess meint, dass ein stellares System dichter wird, indem sich Konstituenten (ohne Zusammenstöße) zu größeren Radien bewegen. Dieser Effekt geschieht im Prinzip auch bei der Entstehung von Kugelsternhaufen, die einzelne Sterne zu höheren Bahnen schicken oder sogar 'herauskicken' und dabei im Zentrum eine hohe Sterndichte annehmen – das Charakteristikum von Kugelsternhaufen. Bei gravitationsgekühlten Bosonensternen werden entsprechend Skalarfelder ausgesandt.

Stabilität

Die Stabilität des Bosonenstern gewährleistet in erster Linie ein fundamentales Prinzip der Quantenphysik: die Heisenbergsche Unschärfe. Im Gegensatz zu Fermionen unterliegen Bosonen nicht dem Pauli-Prinzip. D.h. beliebig viele Bosonen können sich im gleichen Zustand (gleichen Energieniveau) aufhalten. Ist dies der Grundzustand, der bei tiefen Temperaturen erreicht wird, so ist gerade das Bose-Einstein-Kondensat realisiert.
Die Heisenbergsche Unschärferelation besagt auch, dass nicht alle Bosonen innerhalb ihrer Compton-Wellenlänge (siehe Gleichung für λ_C unter Planck-Skala) lokalisiert sein können. Damit stellt Heisenbergs Prinzip einen Druck zur Verfügung, der weitere Kompression des Bosonensterns verbietet.
Falls Wechselwirkung zwischen den Bosonen zugelassen wird, so wirkt auch die abstoßende Kraft zwischen ihnen stabilisierend auf den Bosonenstern.
Eine weitere Aussage zur Stabilität und Zeitabhängigkeit von Bosonensternen macht Derricks Theorem.

Fall 1: Bosonenstern ohne Selbstwechselwirkung

Die einfachste Realisierung eines Bosonensterns ist ein massereiches Klein-Gordon-Feld ohne Selbstwechselwirkung. In diesem Fall reicht die Massenskala dieses speziellen Bosonensterns von 0 bis M_max mit

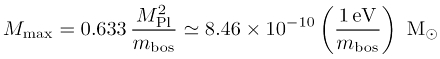
wobei M_Pl die Planck-Masse und m_bos die Bosonenmasse sind. Die Maximalmasse hängt nur von der Masse der Bosonen ab: Je schwerer das Boson, desto kleiner die Maximalmasse. Wie am Ausdruck in Einheiten der Sonnenmasse abzulesen ist, ist die Maximalmasse verglichen mit typischen Sternmassen viel zu wenig. Nur extrem massearme Bosonen würden hier stellare Massen liefern, weshalb man hier auch von Mini-Bosonensternen (engl. mini-boson stars) spricht. Die Obergrenze M_max heißt in der Literatur auch Kaup-Grenze (nach D.J. Kaup 1968).

Fall 2: Bosonenstern mit Selbstwechselwirkung

Lässt man eine Selbstwechselwirkung zwischen den Skalarfeldern zu, so wird es für die Astrophysik schon interessanter. In der Theorie skalarer Felder kann die Bosonen-Selbstwechselwirkung durch einen Term proportional zu Φ⁴ im Lagrangian umgesetzt werden (Colpi et al. 1986). In diesem Fall kann der Bosonenstern so schwer werden wie ein Neutronenstern, d.h. stellare Massen ereichen:

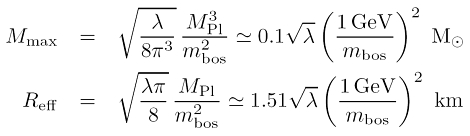
Der Parameter λ gewichtet den Φ⁴-Term. Ist λ groß, so ist die Selbstwechselwirkung zwischen den Bosonen stark. Die Selbstwechselwirkung stabilisiert den Bosonenball.
In der zweiten Zeile ist der Effektivradius des Bosonensterns R_eff angegeben – allerdings in der Näherung Newtonscher Gravitation. Interessanterweise hängt dieser Bosonensternradius nur von der Bosonenmasse, aber nicht von der Bosonensternmasse ab. Mit anderen Worten: ein stellarer Bosonenstern ist genauso groß wie ein supermassereicher Bosonenstern!

Fall 3: rotierende Bosonensterne

Es gibt sogar rotierende Bosonensterne, bei denen der Drehimpuls quantisiert ist. Erstaunlichweise gilt hier die Quantisierung für ein makroskopisches Objekt! Im Gegensatz zur Kugelgestalt des statischen Bosonensterns, wird der rotierende Bosonenstern zu einem Torus (was zumindest aus Symmetriegründen plausibel erscheint). Die Rotation ist differenziell und nicht uniform. Die rotierenden Lösungen der Einstein-Klein-Gordon-Gleichungen ähneln sehr den rotierenden Neutronensternen, nur dass auch die skalare Feldtheorie eingebettet wurde.

Gibt es Bosonensterne – falls ja, wo?

Die astrophysikalisch spannende Frage nach diesen theoretischen Vorbetrachtungen ist, ob im Kosmos Bosonensterne tatsächlich existieren. Gibt es gute Bosonensternkandidaten? Leisten es Bosonensternmodelle andere kompakte Objekte, wie Neutronensterne oder Schwarze Löcher zu ersetzen?
Wir betrachten als Beispiel die schwersten beobachteten supermassereichen Schwarzen Löcher: die elliptische Zentralgalaxie im Virgo-Haufen, M87, enthält ein Loch mit etwa 3 Milliarden Sonnenmassen. Setzen wir dies als Maximalmasse eines Bosonensterns mit Selbstwechselwirkung oben bei M_max ein, so können wir (λ)^1/2(1 GeV/m_bos)² bestimmen und wiederum in R_eff einsetzen. So folgt R_eff ~ 303 AU. Aufgrund der Massenunabhängigkeit von R_eff wäre dieser Wert auch der Radius des Bosonenstern, falls sich ein solcher bei Sgr A*, im Zentrum der Milchstraße, befinden würde. Beobachtungen besagen jedoch, dass Sgr A* kleiner als 60 AU sein muss, so dass in diesem Fall ein Bosonenstern (zumindest in diesem einfachen Bosonensternmodell) ausgeschlossen sein muss. Ähnliches gilt für die superschweren, kompakten und dunklen Objekte in Aktiven Galaktischen Kernen, für die etwa R ≤ 7 AU gilt. Damit müssen supermassereiche Schwarze Löcher als kompakte, dunkle Objekte in den Zentren von Galaxien favorisiert werden (nach Bilic 2007). Dennoch mögen im ein oder anderen Fall Bosonensterne in Frage kommen. Weiterhin werden alternativ zu Bosonensterne die Fermionensterne diskutiert. In der Community der Astronomen werden Schwarze Löcher im Allgemeinen favorisiert.

Quellen & wissenschaftliche Veröffentlichungen

• Kaup, D.J.: Klein-Gordon Geon, Phys. Rev. 172, 1331, 1968
• Colpi et al.: Boson stars: Gravitational equilibria of self-interacting scalar fields, Phys. Rev. Lett. 57, 2485, 1986
• Seidel, E. & Suen, W.-M.: Formation of solitonic stars through gravitational cooling, Phys. Rev. Lett. 72, 2516, 1994
• Jetzer, P.: Boson stars, Phys. Rep. 220, 163, 1992
• Schunck, F.E. & Mielke, E.W: General relativistic boson stars, Class. Quant. Grav. 20, R301, 2003
• Bilic, N.: Black-Hole Phenomenology, Lecture Notes at Dubrovnik Summer School, Proceedings of Science (P2GC) 004, 2007; Preprint: gr-qc/0109035