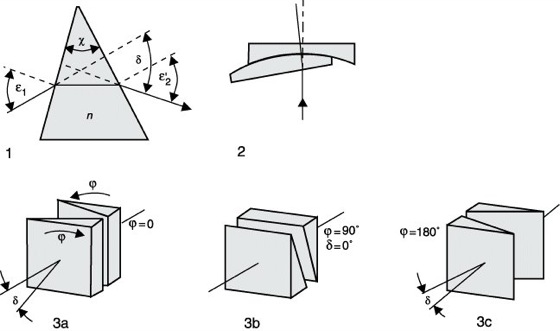
Ablenkprisma, brechender Keil, ein Prisma, das zur Ablenkung eines Lichtstrahles um kleine Winkel dient. Ein im Hauptschnitt (Prisma) auf die brechende Ebene fallender Lichtstrahl bleibt bei der Brechung innerhalb des Hauptschnittes. Der Ablenkwinkel δ hängt ab vom Prismenwinkel ω, vom Einfallswinkel ε₁ des Lichtstrahles sowie vom Brechungsindex n des Prismenmaterials und errechnet sich aus der Gleichung δ=ε₁+ε'₂-ω; dabei ist

(Teilabb. 1). Bei symmetrischem Durchgang wird δ minimal (Minimum der Ablenkung).

Sind Einfallswinkel und Prismenwinkel klein, gilt in guter Näherung δ=ω(n-1). Infolge der brechenden Wirkung des A. tritt immer eine Beeinflussung der Abbildung ein. Die Dispersion bewirkt einen Farbfehler, der sich bedingt beheben läßt (achromatisches Prisma). Ferner entstehen Fehler hinsichtlich der Maßstabstreue, die sich als Bildverzerrung im Hauptschnitt auswirken. Weiterhin tritt eine Bilddrehung zum Hauptschnitt ein.

Anwendung, in der Regel für kleine Ablenkwinkel, finden A. als Justierhilfsmittel zum Ausgleich unvermeidbarer Herstellfehler bei Präzisionsinstrumenten sowie zu Meßzwecken, wobei sie häufig als veränderliche Keile ausgeführt sind. Dazu gehören:

Abatscher Keil oder Schwenkkeil (Teilabb. 2), ein auf M. Boscovich (1777) zurückgehendes A., bestehend aus einer plankonkaven Linse, in deren Kugelfläche sich eine plankonvexe Linse mit gleichem Radius und gleicher Brechung dreht. Beide Linsenwirkungen heben sich gegenseitig auf. Diese Anordnung kann auch aus entsprechenden Zylinderlinsen hergestellt sein.

Beim Schwingkeilpaar wird zur Veränderung der Ablenkung deren Abhängigkeit vom Einfallswinkel benutzt. Zu diesem Zwecke werden zwei gleiche Keile um eine Parallele zu den brechenden Kanten gedreht.

Drehkeilpaar, auch Herschelsches Doppelprisma, Keilkompensator oder Diasporameter genannt (Teilabb. 3). Es beruht auf folgendem Prinzip: Dreht man zwei gleiche Keile in entgegengesetzter Richtung um eine gemeinsame Achse im Hauptschnitt, so erhält man die Wirkung eines veränderlichen Keils. Zählt man die Verdrehung ϕ von der Lage der größten Ablenkung aus (Gesamtablenkung gleich Summe beider Einzelablenkungen), so gilt für die jeweilige Ablenkung δ=2δ_kcosϕ (δ_k Ablenkung des Einzelkeils). Das Drehkeilpaar ist die von allen A. vorwiegend angewendete Anordnung. Die Abhängigkeit des Ablenkwinkels vom Drehwinkel ist in einem mittleren Bereich (45°

ϕ

135°) praktisch linear, wobei der Drehwinkel ein Vielfaches (das 15- bis 20fache) des Ablenkwinkels beträgt. Diese Tatsache wird oft beim Bau von Entfernungsmessern ausgenutzt. – Das Meßlinsenpaar ist eine dem Abatschen Keil ähnliche Kombination zweier Linsen, bei der jedoch keine Drehung, sondern eine Verschiebung senkrecht zur optischen Achse vorgenommen wird. Hierbei tritt ähnlich wie bei dem veränderlichen Keil eine Ablenkung des austretenden Strahles ein. Für den Ablenkwinkel δ gilt im Falle gleicher Brennweite f der beiden Linsen tanδ=v/f, wobei ν die Größe der Verschiebung bezeichnet. Das Meßlinsenpaar wird für meßtechnische Zwecke angewendet.

Bei der teleskopischen Abbildung eines zum Hauptschnitt senkrechten Spaltes über ein A. wird seine scheinbare Länge nicht verändert. Die scheinbare Breite wird aber durch die Winkelvergrößerung im Hauptschnitt bestimmt. Diese ist nur im Minimum der Ablenkung wegen der Symmetrie der Brechungen gleich 1, d.h., nur hier bleibt die Breite unverändert. Zwischen streifendem Eintritt und streifendem Austritt durchläuft die Winkelvergrößerung die Werte Null bis Unendlich, es tritt also im Hauptschnitt eine vom Einfallswinkel abhängige Vergrößerung ein. Als Folge ergibt sich eine Bildveränderung (Bildverzerrung).

Für senkrechten Einfall und eine Winkelvergrößerung γ errechnet sich der brechende Winkel ω des Prismas aus der Beziehung


und die Ablenkung δ aus


.

Setzt man zwei gleiche Prismen so hintereinander, daß ihre Ablenkung entgegengesetzt ist, erhält man ein geradsichtiges System mit der Winkelvergrößerung γ² (Anwendung bei der Breitwandprojektion). Fügt man ein weiteres gleiches System ein, dessen Hauptschnitt gegen den des ersten um 90° gedreht ist, entsteht ein aus 4 Prismen bestehendes Fernrohr.

Ablenkprisma: 1 gewöhnliches Ablenkprisma, 2 Abatscher Keil, 3 Drehkeilpaar. δ Ablenkwinkel.