elektromagnetische Welle, ein im Vakuum oder einem nichtabsorbierenden Medium sich ausbreitendes elektromagnetisches Feld. Zu den e. W. zählen im besonderen die Lichtwellen. An jedem Orte führen die elektrische Feldstärke E und die magnetische Feldstärke H Schwingungen der Dauer T=1/ν aus, die in der Optik als Lichtperiode bezeichnet wird. Die Frequenz ν ist dabei an allen Orten die gleiche. Die Amplitude ist ebenfalls konstant, oder ändert sich jedenfalls erst über größere Entfernungen merklich. Dagegen zeigt die Phase der Schwingungen, worunter das volle Argument des Kosinus in der Gleichung für die harmonische Schwingung zu verstehen ist, eine starke Ortsabhängigkeit. Orte gleicher Phase (bei festgehaltener Zeit) bilden eine Phasen- oder Wellenfläche, auch Wellenfront genannt. Der Abstand zweier Phasenflächen, die sich in der Phase um 2π unterscheiden, ist die Wellenlänge λ. Wegen des Vektorcharakters von E und H sind e.W. polarisiert (Polarisation 1)).

Die Wellenausbreitung besteht in einer zeitlichen Verschiebung der Phasenflächen. Die Normale zu den Phasenflächen (Wellennormale), zeigt die Ausbreitungsrichtung an. Die Geschwindigkeit, mit der eine konstante Phase in Ausbreitungsrichtung fortschreitet, heißt Phasengeschwindigkeit. Sie ist von der Gruppengeschwindigkeit zu unterscheiden. Die Phasengeschwindigkeit im Vakuum, die Vakuumlichtgeschwindigkeit c, ist frequenzunabhängig. In optischen Medien hängt die Phasengeschwindigkeit in der Regel von der Frequenz ab, d.h., es liegt Dispersion vor.

Der in die Ausbreitungsrichtung zeigende Vektor der Länge 2π/λ wird Wellenzahlvektor k genannt. Entsprechend bezeichnet man die Größe 2π/λ als Wellenzahl k. Diese Bezeichnung ist jedoch nicht einheitlich; in der Spektroskopie versteht man unter der Wellenzahl die Größe 1/λ. Wellenlänge λ, Frequenz ν und Phasengeschwindigkeit u stehen in dem Zusammenhang u=ν·λ. Bei dem Übergang einer e. W. von einem Medium in ein anderes, in dem die Phasengeschwindigkeit einen anderen Wert besitzt, ändert sich die Frequenz nicht, wohl aber die Wellenlänge.

Mit der Wellenausbreitung ist auch ein Energietransport verbunden, der durch den Poynting-Vektor S (Maxwellsche Gleichungen) beschrieben wird. Die Intensität I der Strahlung entspricht dem Betrag des über einige Lichtperioden gemittelten Vektors S. Für sie gilt:


,

gemessen in W/m², mit ε₀ als der Dielektrizitätskonstanten des Vakuums und n als dem Brechungsindex des Mediums. Diese Gleichung ist auch für stehende Wellen (s.u.) gültig, obwohl dort keine Energieströmung stattfindet. Die relative Intensität ist allein durch

gegeben.

Die Richtung des Energieflusses (d.h. des Poynting-Vektors) wird Strahlrichtung genannt. Sie stimmt bei isotropen Medien mit der Ausbreitungsrichtung überein, bei anisotropen jedoch nicht (Kristalloptik).

Aus den Maxwellschen Gleichungen ergibt sich für die kartesischen Komponenten E_j(j=x,y,z) des Feldstärkevektors E eine Wellengleichung der Form


(1)

deren Lösungen die verschiedenen Typen von e. W. beschreiben.

Mit dem Ansatz


(2)

ergibt sich die zeitfreie Wellengleichung


(3)

mit ω=2πν als der Kreisfrequenz und A_j(x,y,z) als der ortsabhängigen komplexen Amplitude der elektrischen Feldstärke.

Man erhält als Lösung von (1) zunächst komplexe Werte für E_j. Durch Bildung des Realteils wird hieraus die physikalisch allein sinnvolle Lösung gewonnen. Zu beachten ist, daß die Schreibweise für den zeitabhängigen Faktor in (2) nicht einheitlich ist, manche Autoren verwenden auch exp(iωt).

Den einfachsten Wellentyp stellt die linear polarisierte, monochromatische ebene Welle dar. Bei ihr sind die Wellenflächen Ebenen. Eine solche e. W. möge sich in z-Richtung ausbreiten und in x-Richtung polarisiert sein, dann gilt:


, (4)

wobei A eine konstante, im allgemeinen komplexe Amplitude, ε die Dielektrizitätskonstante des Mediums und μ dessen Permeabilität bezeichnen.

Neben ebenen Wellen sind in der Optik auch Kugel- und Zylinderwellen von Bedeutung, die kugel- bzw. zylinderförmige Wellenflächen besitzen. Hier sieht man häufig von der Polarisation der e. W. ab und ersetzt demgemäß den elektrischen Feldstärkevektor durch eine skalare Größe ψ. Die Kugelwelle kann damit in folgender Form beschrieben werden:


. (5)

Dabei bedeutet r den Abstand vom Zentrum der Kugelwelle. Dem Pluszeichen im Exponenten entspricht eine auslaufende, dem Minuszeichen eine einlaufende Kugelwelle.

Für Zylinderwellen gilt: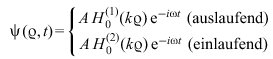


(6)

mit

als den Hankel-Funktionen 1. bzw. 2. Art der Ordnung 0; ρ bezeichnet den Abstand von der Zylinderachse.

Des weiteren stellen Gaußsche Bündel eine spezielle, für die Optik bedeutsame Wellenform dar.

Neben den laufenden Wellen gibt es auch stehende Wellen, die sich durch die Überlagerung gegenläufiger Wellen, z.B. durch senkrechte Reflexion an einem Spiegel (Wienersche Interferenzen) erzeugen lassen. Sie bilden sich auch in optischen Resonatoren aus. Bei stehenden Wellen ist die Schwingungsphase allenfalls nur sehr schwach ortsabhängig, dafür ändert sich die elektrische Feldstärke räumlich außerordentlich stark. Es treten Knotenflächen auf, d.h. Flächen, auf denen die elektrische Feldstärke verschwindet. Der Abstand zwischen zwei benachbarten Knotenflächen beträgt λ/2. In der Mitte zwischen ihnen befinden sich die Wellenbäuche mit maximaler elektrischer Feldstärke. Speziell für eine linear polarisierte stehende ebene Welle kann geschrieben werden:


(7)

E. W. durchdringen einander, ohne sich gegenseitig zu stören. (Bei sehr hohen Feldstärken gilt dies allerdings nur für das Vakuum; nichtlineare Optik.) Bei der Durchdringung addieren sich die elektrischen Feldstärken zu einer Gesamtfeldstärke. Auf diesem Superpositionsprinzip beruhen die Erscheinungen der Interferenz.

Im optischen Frequenzbereich werden e. W. durch spontane oder induzierte Emission von den unterschiedlichsten Lichtquellen erzeugt.