Metalloptik, die Lehre von den optischen Eigenschaften der Metalle. Sie ist auf der Grundlage der klassischen Elektronentheorie der Metalle von P. Drude und mittels der Quantentheorie von R. Kronig behandelt worden. Die Elektronen im Metall sind zum Teil frei (Leitungselektronen), zum Teil an eine Ruhelage elastisch gebunden. Die elektrische Feldstärke des einfallenden Lichtes erzeugt im Metall einen elektrischen Strom, dessen Träger die freien Elektronen sind und der auf Grund des elektrischen Widerstandes des Metalles Ohmsche Verluste erleidet. Auf diese Weise wird letztlich Energie aus dem Strahlungsfeld an das Gitter der Metallionen abgegeben. Die Strahlung erfährt so eine starke Dämpfung und kann nur bis zu einer geringen Tiefe in das Metall eindringen, die in der Regel nur einen sehr kleinen Bruchteil einer Wellenlänge ausmacht (Gl. (5)). (Bei Kupfer z.B. beträgt die Eindringtiefe im UV-Bereich bei 100 nm Vakuumwellenlänge nur 0,62 nm.) Man beschreibt diesen Dämpfungsvorgang durch Einführung einer komplexen relativen Dielektrizitätskonstanten

_r, die sich aus den Maxwellschen Gleichungen zu


(1)

ergibt. Dabei bezeichnen ε_r die reelle relative Dielektrizitätskonstante, ε₀ die Dielektrizitätskonstante des Vakuums, σ die Leitfähigkeit des Metalls und ω die Kreisfrequenz der Strahlung. (Man beachte, daß das Vorzeichen vor dem Faktor i in (1) und ebenso in (2) und (6) davon abhängt, wie man die komplexe Amplitude des elektrischen Feldes definiert. Die hier getroffene Vorzeichenwahl bezieht sich auf die Zeitabhängigkeit exp(-iωt); elektromagnetische Welle). Auch der Brechungsindex wird komplex; man schreibt ihn in der Form:


(2)

mit n als reellem Brechungsindex. Man nennt Κ' häufig den Absorptionsindex und das Produkt Κ=nΚ' nach DIN die spektrale Absorptionszahl (Absorptionskoeffizient). Aus der MaxwellschenBeziehung

mit μ_r als relativer Permeabilität erhält man die beiden Relationen:


(3)

die sich auf


(4)

reduzieren, da in praxi σ/(2ε₀ω) sehr viel größer als ε_r ist.

Aus n und Κ' läßt sich der Reflexionsgrad ρ berechnen (Reflexion). Die optischen Konstanten einiger Metalle sind in der Tabelle aufgeführt.

Für die Eindringtiefe des Lichtes gilt allgemein:


(5)

mit λ als Wellenlänge im Metall.

In der klassischen Drudeschen Theorie des freien Elektronengases werden die Elektronen durch die elektrische Feldstärke des Lichtfeldes wie freie Teilchen beschleunigt, durch Stöße mit den Metallionen jedoch abgebremst. Dadurch kommt es zu einem Mitschwingen der Elektronen mit der Lichtfrequenz, und es tritt eine Polarisation des Mediums auf, die eine Abweichung der Dielektrizitätskonstanten von ihrem Vakuumwert zur Folge hat. Die relative Dielektrizitätskonstante ergibt sich so zu dem komplexen Wert:


(6)

Dabei bedeuten e die Ladung und m die Masse des Elektrons, N_f die Zahl der freien Elektronen in der Volumeneinheit und δ_f die Dämpfungskonstante für die Elektronenbewegung, die gleich der Stoßfrequenz (Zahl der Stöße pro s) ist. Mit der Plasmafrequenz


(7)

ergeben sich für μ_r=1 die Relationen: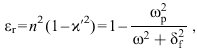


(8)


(9)

Typische Werte für die Stoßfrequenz und die Plasmafrequenz sind δ_f≈10¹³/s und ω_p≈10¹⁵/s. Die Frequenzen der sichtbaren sowie der infraroten Strahlung liegen dazwischen. Nach (8) und (9) ist dann ε_r negativ (das bedeutet, daß die Elektronen gegenphasig zum elektrischen Feld schwingen) und Κ' groß (Tab.). Mit der starken Dämpfung ist ein hohes Reflexionsvermögen verknüpft, und die bei schrägem Einfall von linear polarisiertem Licht reflektierte Strahlung ist elliptisch polarisiert (Reflexion, Ellipsometrie). Für ω

ω_p wird jedoch ε_r positiv und Κ' klein, d.h., das Metall wird wieder durchsichtig. Ein solches Verhalten wird an den Alkalimetallen im UV-Bereich tatsächlich beobachtet.