sphärische Aberration, Öffnungsfehler, zum Hauptstrahl (Blende) symmetrische Aberration, bei der sich nur alle diejenigen vom Objektpunkt ausgehenden Strahlen, die die gleiche Pupillenhöhe h_B haben und auf einem Kegelmantel axialsymmetrisch zum Hauptstrahl liegen, in einem gemeinsamen, gegenüber der Gaußschen Bildebene defokussierten Punkte schneiden (Abb. 1a). Da diese als sphärische Längsaberration bezeichnete Defokussierung näherungsweise zu h²_B proportional ist, entsteht statt des Bildpunktes eine zum Hauptstrahl axialsymmetrische Kaustik, die in der Bildebene einen bei großem Bildwinkel elliptisch deformierten Zerstreuungskreis erzeugt, der durch Abblenden verkleinert wird. Bei der optischen Abbildung außeraxialer Punkte ist die s. A. meist von Koma (Abb. 1b) und Astigmatismus überlagert.

Im Gegensatz zu den übrigen Aberrationen tritt die s. A. isoliert bei der Abbildung axialer Objektpunkte durch Strahlenbündel mit endlichem bildseitigen Öffnungswinkel σ

auf, da jede Zone eines optischen Systems eine andere Brechkraft und damit eine andere bildseitige Schnittweite

besitzt, so daß der bildseitig axiale Strahlenschnittpunkt von der Strahlneigung σ' bzw. von h_B abhängt (Abb. 2). Der näherungsweise

proportionale Abstand

ist die bei Sammellinsen negative (Unterkorrektion) bzw. bei Zerstreuungslinsen positive sphärische Längsaberration des axialen Bildpunktes, die meist als Funktion von h_B graphisch dargestellt wird (Abb. 2c, 3c und 4c). Günstiger ist die Angabe der sphärischen Queraberration Δy'=Δs'tanσ', deren Maximalwert dem Halbmesser des Zerstreuungskreises in der Gaußschen Bildebene entspricht. Durch Einzeichnung der Schmiegungsgeraden b'_Ktanσ' an die Queraberrationskurve Δy'(tanσ') (Abb. 2b, 3b und 4b) findet man die um b

gegenüber der Gaußschen Bildebene defokussierte Auffangebene kleinster Zerstreuung. Bei s. A. 3. Ordnung

liegt diese Auffangebene besten Kontrastes oder minimalen Gauß-Momentes bei 2/3 der durch den Randstrahl definierten, auf die Gaußsche Bildebene bezogenen maximalen sphärischen Längsaberration von

(B₃Lukosz-Koeffizient für die s. A. 3. Ordnung, n' Bildraumbrechzahl, ρ' auf den Pupillenradius bezogene Höhe in der Austrittspupille).

Der Zerstreuungskreis und das Gauß-Moment reduzieren sich dabei auf 1/3 bzw. 1/9. Die Auffangebene maximaler Definitionshelligkeit ist um 0,5 Δs

gegenüber der Gaußschen Bildebene defokussiert, wobei sich der Zerstreuungskreis und das Gauß-Moment auf 50% bzw. 17% reduzieren (Abb. 2). Bei s. A. 3. und 5. Ordnung mit korrigiertem Randstrahl

(B₅ Lukosz-Koeffizient für überlagerte s. A. 3. und 5. Ordnung) ist die Auffangebene bester Definitionshelligkeit um 4/5 des für die Pupillenzone

auftretenden Zonenfehlers von

unter Vergrößerung des Zerstreuungskreises um etwa 10% und Verkleinerung des Gauß-Momentes auf 20% defokussiert. Die Auffangebene besten Kontrastes, in der sich der Zerstreuungskreis auf 90% und das Gauß-Moment auf 17% reduzieren, ist um 2/3 Δs'_z gegenüber der Gaußschen Bildebene defokussiert (Abb. 3).

Den absolut besten Kontrast erhält man bei s. A. 3. und 5. Ordnung, wenn man den für

auftretenden Zonenfehler auf

vergrößert, den Randstrahl mit

unterkorrigiert und die Auffangebene um

defokussiert:


(Abb. 4).

Die Lage der günstigsten Auffangebene ist vom Kohärenzparameter abhängig, wenn dieser kleiner als 0,4 ist.

Die Korrektion der s. A. erfolgt durch Durchbiegung (Abb. 5) und durch Kombination von Sammel- und Zerstreuungslinsen, deren s. A. sich bis auf Zonenfehler kompensieren. Durch s. A. entsteht eine Wellenaberration der Größe l'(ρ') = 〈l'〉 + A₂₀(2ρ'² – 1) + A₄₀(6ρ'⁴ – 6ρ'² + 1) + A₆₀(20ρ'⁶ – 30ρ'⁴ + 12ρ'² – 1) + ... (A₂₀, A₄₀ und A₆₀Nijboer-Zernike-Koeffizienten, die sich auf Defokussierung gegenüber der Auffangebene größter Definitionshelligkeit, s. A. 3. Ordnung und s. A. überlagerter 3. und 5. Ordnung jeweils beziehen; 〈l'〉=A₂₀-A₄₀+A₆₀+... mittlere Wellenaberration), die die Definitionshelligkeit auf

verringert. Für beugungsbegrenzte Systeme mit V≥0,8 gilt für s. A. 3. Ordnung |A₄₀|≤0,16 λ₀ bzw. für s. A. 3. und 5. Ordnung |A₆₀|≤0,19 λ₀ (λ₀ Vakuumwellenlänge).

Die s. A. der Hauptstrahlen ist die Pupillenaberration.

Sphärische Aberration 1: Reine (a) und von Koma überlagerte (b) sphärische Aberration bei der Abbildung durch eine Kugelfläche. C Krümmungsmittelpunkt, F' Brennpunkt.

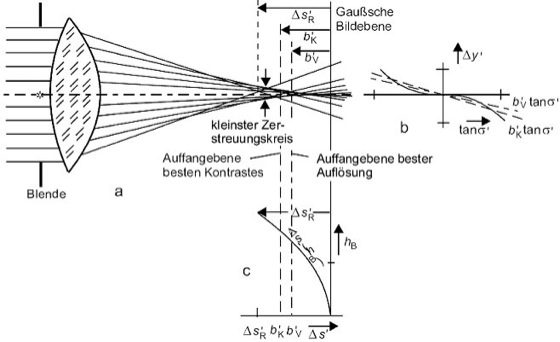
Sphärische Aberration 2: Sphärische Aberration 3. Ordnung

. Strahlengang (a) und graphische Darstellung der Quer- (b) und Längsaberrationen (c). h_B Pupillenhöhe, σ' Strahlneigung.

Sphärische Aberration 3: Sphärische Aberration 3. und 5. Ordnung

mit Randkorrektion. Strahlengang (a) und graphische Darstellung der Quer- (b) und Längsaberrationen (c).

Sphärische Aberration 4: Sphärische Aberration 3. und 5. Ordnung

mit Randstrahlunterkorrektion

. Strahlengang (a) und graphische Darstellung der Quer- (b) und Längsaberration (c).

Sphärische Aberration 5: Einfluß der Durchbiegung einer Linse auf die sphärische Aberration. h_B Höhe in der Eintrittspupille.