Strahlmatrix, ABCD-Matrix, quadratische Matrix vom Rang 2 mit den Elementen A, B, C, D, die in der Form

mit i=x,y

die Transformation der Richtung

und der Lage

eines Lichtstrahls von einer beliebigen achsenorthogonalen Eingangsebene (E) in eine beliebige achsenorthogonale Ausgangsebene (A) bei der optischen Abbildung beschreibt. Dabei sind die cosα_iE für i=x, y, z die Richtungskosinusse des Strahlrichtungseinheitsvektors s_0E und die h_iE für i=x, y die Koordinaten des Durchstoßpunktes des Strahls in der Eingangsebene sowie cosα_iA und h_iA die entsprechenden Größen in der Ausgangsebene. Die Brechzahlen in beiden Durchstoßpunkten sind n_E und n_A.

Für die Brechung an einer Kugelfläche (m) mit dem Radius r_m sowie n_E=n_m und n_A=n'_m=n_m+1 existiert eine Brechungsstrahlmatrix R_m mit den Komponenten

und

. Der Einfallswinkel ε_m und der Brechungswinkel ε'_m berechnen sich über das vektorielle Brechungsgesetz entsprechend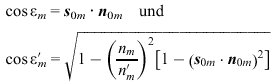

aus den Skalarprodukten der Einheitsvektoren s₀ und n₀ in Richtung des Strahls und der Flächennormalen im Einfallspunkt der Fläche (m).

Die Elemente der Translationsstrahlmatrix T_m für den Übergang zur Nachbarfläche (m+1) sind


.

Der Abstand beider Strahldurchstoßpunkte ist d

_m. Auch die Übergänge von der Objektebene sowie zu und von den Pupillen und zur Bildebene lassen sich durch Translationsstrahlmatrizen beschreiben.

Für die Strahltransformation von der Objektebene (O) mit den Parametern n_E=n_O, cosα_iE=cosα_iO (Objektraumstrahlneigung) und h_xE=x_O, h_yE=y_O (Objektpunktkoordinaten) in die Bildebene (Κ+1) mit den Parametern

(Bildraumstrahlneigung) und

durch ein optisches System aus Κ Flächen kann aus Κ+1 Translationsstrahlmatrizen T_m für die Übergänge von der Objektebene, zwischen den brechenden Flächen und zur Bildebene sowie aus den Κ Brechungsstrahlmatrizen R_m der brechenden Flächen durch nicht kommutative Matrizenmultiplikation eine einem konkreten Strahl zugeordnete Produktstrahlmatrix

gebildet werden.

Besonders vorteilhaft ist die Anwendung von S. für das Optikrechnen im paraxialen Gebiet. Wegen

(paraxiale Strahlneigung),

(paraxiale Bildhöhe) sind alle Elemente der als Gauß-Matrizen bezeichneten paraxialen S. strahlunabhängige Funktionen der Brechzahlen, Radien, Linsendicken und -abstände d'_m sowie der paraxialen Schnittweiten s₀₁ und s'₀Κ im Objekt- und Bildraum. Die Matrixelemente der Gauß-Matrizen sind

und


.

Im paraxialen Gebiet kann man jeder dünnen Linse (L) eine Brechungsstrahlmatrix zuordnen, deren Element

der negativen Brechkraft der Linse entspricht (f

Brennweite der Linse).

Auch asphärischen Linsen, axialsymmetrischen Gradientenindexlinsen, Gittern und im erweiterten Sinne Interferenzschichten können S. zugeordnet werden. Das Zusammenwirken mehrerer derartiger optischer Bauelemente kann durch die beschriebene Multiplikation entsprechender Matrizen in paraxialer Näherung mathematisch modelliert werden. Ein weiteres Anwendungsgebiet der S. ist die Strahltransformation Gaußscher Bündel.