Kosmologie

Gerhard Börner, Garching

1 Einleitung

Die Kosmologie ist eine ganz besondere Wissenschaft. Ihr Forschungsgegenstand ist die Struktur und Dynamik des Universums als Ganzes. Definitionsgemäß befaßt sie sich mit einem einzigartigen Objekt und einem einzigartigen Ereignis. Jeder Physiker wäre unglücklich, müßte er seine Theorien auf ein einzelnes, unwiederholbares Experiment stützen. Doch es konnte trotzdem eine wissenschaftliche Kosmologie formuliert werden, weil das beobachtete Universum in seiner großräumigen Struktur sehr einfach ist, einfacher als man erwarten konnte. Darüber hinaus erfährt der Astronom wegen der endlichen Lichtgeschwindigkeit durch die Beobachtung weit entfernter Objekte etwas über den Kosmos zu früheren Zeiten. Schwierig ist die Situation natürlich auch deswegen, weil wir, die Beobachter, mitten in diesem Objekt ›Universum‹ nur einen räumlich und zeitlich begrenzten Ausschnitt wahrnehmen, von dem wir zwar annehmen, daß er für das Ganze – wenn es das überhaupt gibt – repräsentativ ist, es aber nicht sicher wissen können. Der Kosmologe muß also zusätzlich zu den vorhanden Beobachtungen und Meßergebnissen Theorien voraussetzen, um die Beobachtungen zu deuten und neue Untersuchungen vorzuschlagen. So entsteht ein Modell des Kosmos.

2 Zwei wichtige Entdeckungen

Das moderne Bild vom Kosmos beruht im wesentlichen auf zwei fundamentalen Beobachtungen: die erste war die Entdeckung des amerikanischen Astronomen E.P. Hubble, daß sich fast alle fernen Galaxien von uns weg bewegen, und zum andern auf der Messung eines kosmischen Strahlungsfeldes im Mikrowellenbereich durch A.A. Penzias und R. Wilson im Jahre 1964. Hubble fand, daß fast jede Galaxie (außer einigen sehr nahen) eine Verschiebung ihrer Spektrallinien zu größeren Wellenlängen zeigt, die um so größer ist, je weiter die Galaxie entfernt ist:

(λ_b: beobachtete, λ_e: ausgesandte Wellenlänge). Die Erklärung dieser Rotverschiebungz durch den Dopplereffekt führt zu dem Schluß, daß die Galaxien sich von uns wegbewegen (Hubble-Fluß). Das Bild der Welt hat sich durch Hubbles Entdeckung dramatisch verändert: Die Vorstellung einer gleichmäßigen, unveränderlichen Verteilung von Sternen bis in unendliche Tiefen, ein Bild, dem zunächst sogar Albert Einstein vertraut hatte, mußte aufgegeben werden zugunsten der Idee eines Universums der Entwicklung und Veränderung, wie es das auseinanderfliegende, expandierende System der Galaxien darstellt. Die zweite wichtige Entdeckung war die der Hintergrundstrahlung mit der Temperatur

K, die der im November 1989 gestartete NASA-Satellit COBE besonders genau vermessen hat (siehe Abb.1 ). Sie wird von den meisten Fachleuten als Hinweis auf einen Anfangszustand angesehen, in dem das Universum so heiß und dicht war, daß die Atome in ihre Kerne und Elektronen aufgelöst waren und die Streuung von Photonen an freien Elektronen das thermische Gleichgewicht zwischen Strahlung und Materie aufrechterhielt. Bemerkenswert ist die hohe Isotropie dieser Strahlung. Andererseits spiegeln die Anisotropien Dichteschwankungen von etwa gleicher Amplitude wider, die als Ursachen und Keime für die beobachteten Strukturen der leuchtenden Materie angesehen werden.

3 Die kosmologischen Modelle

Die Unsicherheiten der astronomischen Messungen lassen Raum für eine ganze Reihe von Modellen, die auch qualitativ verschieden sind. Trotzdem sprechen die Astronomen von einem ›Standard-Urknall-Modell‹ im Sinne einer ganzen Klasse von Modellen, die einige typische Eigenschaften gemeinsam haben: Das Universum hat sich nach einer explosionsartig schnellen Ausdehnung zu Anfang durch eine heiße und dichte Frühphase zum gegenwärtigen Zustand entwickelt. Es ist homogen und isotrop auf großen Skalen. Strukturen wie Galaxien und Galaxienhaufen haben sich aus anfänglich kleinen Dichteschwankungen durch die Wirkung der Schwerkraft gebildet. Es ist bemerkenswert, wie weit diese einfachen Konzepte tragen. Bis jetzt hat sich keine alternative Theorie gezeigt, die alle Beobachtungen der kosmischen Struktur und Evolution ähnlich gut wie das Standardmodell erklärt.

Die Basis der klassischen kosmologischen Modelle ist die Allgemeine Relativitätstheorie Einsteins, eine Theorie der Schwerkraft, die bis jetzt alle experimentellen Tests glorreich bestanden hat. Es gibt drei große Vorzüge der Allgemeinen Relativitätstheorie im Vergleich zur Newtonschen Theorie, besonders im Hinblick auf die Kosmologie: 1. Die Gravitationswirkung einer unendlichen Massenverteilung kann ohne Probleme beschrieben werden. (In der Newtonschen Theorie ist das Gravitationspotential in einem derartigen Fall nicht eindeutig durch die Massenverteilung bestimmt.) 2. Die Theorie hat Lösungen, die als einfache Modelle des Universums angesehen werden können, wie etwa ein abgeschlossener, endlicher Raum ohne Grenze. 3. Die Lichtausbreitung wird im Einklang mit den Experimenten beschrieben.

Die aus der Hintergrundstrahlung erschlossene Gleichförmigkeit der Welt zusammen mit der allgemeinen Expansion legen eine einfache Interpretation in den sog. Friedmann-Lemaître (FL)- Modellen (nach Friedmann (1922) und Lemaître (1927), die zum ersten Mal Lösungen aus Einsteins Gravitationstheorie abgeleitet haben) nahe. Als einfache, hochsymmetrische Lösungen der Theorie sind sie geeignete mathematische Modelle für das gleichmäßig expandierende Universum.

Ausgehend vom jetzigen Zustand läßt sich mit Hilfe der FL-Modelle die Geschichte des Kosmos theoretisch rekonstruieren. Es werden natürlich wegen der Homogenität der Modelle nur zeitliche Veränderungen erfaßt und schon aus diesem Grund können die FL-Modelle nur angenähert gültig sein. Aus den Lösungen der FL-Gleichungen läßt sich entnehmen (siehe Abb. 2 ), daß der Expansionsfaktor

vor einer endlichen Zeit gleich Null war. Bei Annäherung an diesen Zeitpunkt, beim Rückgang in die Vergangenheit, wachsen Dichte und Ausdehnungsrate über alle Grenzen. Man kann deshalb die Entwicklung nicht weiter theoretisch zurückverfolgen, weil die Begriffe und Gesetze der Theorie ihren Sinn verlieren. Diese Anfangssingularität kennzeichnet den Anfang der Welt. Alles, was wir jetzt beobachten, ist vor 10 bis 20 Milliarden Jahren in einer Urexplosion entstanden, die von unendlicher Dichte, Temperatur und unendlich großem Anfangsschwung war. Kurz nach diesem als Urknall bezeichneten Ereignis können wir versuchen, die Welt mit der uns bekannten Physik zu beschreiben, und die zeitliche Abfolge verschiedener physikalisch unterschiedlicher Phasen darzustellen (kosmologische Epochen).

Zur quantitativen Festlegung eines bestimmten kosmologischen Standardmodells benötigt man außer der Hubble-Konstanten

(bzw. dem dimensionslosen Parameter h = H₀ / (100 km s^-1Mpc^-1)), die die momentane Expansionsgeschwindigkeit angibt, noch zwei Parameter. Geeignet sind etwa die Dichteparameter

und

(kosmologische Konstante) und das Weltalter

.

4 Die Hubble-Konstante H₀

Die Hubble-Konstante präzise zu messen ist schwierig, denn alle Galaxien weisen zufällige Eigenbewegungen auf von einigen 100 km s^-1, da sie zumeist in größere Strukturen eingebunden sind, deren Gravitationsfeld ihre Bewegung beeinflußt. Dies wirkt sich besonders für nahe Objekte aus, während bei weit entfernten Galaxien die Expansionsbewegung völlig überwiegt. Bei diesen allerdings sind die Entfernungsbestimmungen sehr ungenau. Dies ist wohl der Grund dafür, daß viele Jahre hindurch die Beobachter in zwei Lager gespalten waren, die jeweils für eine große Entfernungsskala (H₀

50 km s^-1 Mpc^-1) oder für eine kleine (H₀

100 km s^-1 Mpc^-1) votierten. Beide Resultate wurden üblicherweise mit sehr kleinen Fehlern angegeben (kleiner als 10 %). Man erwartete, daß die Situation sich entscheidend verbessern würde, wenn durch neue Teleskope, speziell durch das Hubble-Weltraumteleskop, Cepheidensterne (Cepheiden) in Entfernungen von mehr als 20 Mpc beobachtbar würden, z.B. im Virgohaufen. Die Bestimmung von H₀ durch die Vermessung des Virgohaufens ist aber wegen der Komplexität dieses Gebildes durch relativ große sowohl systematische als auch beobachtungsbedingte Fehler behaftet, so daß diese Methode nicht sehr geeignet dafür ist, präzise Werte für H₀ zu erhalten.

Eine andere Methode, die sehr vielversprechend erscheint und an der in den letzten Jahren aktiv gearbeitet wurde, nutzt Supernovae vom Typ Ia, um die Sprossen der Entfernungsleiter zu überspringen und direkt Meßpunkte jenseits des Virgohaufens zu erhalten, bei denen lokale Geschwindigkeitsfelder keine Rolle mehr spielen. Man versucht im Augenblick eine möglichst gute Eichung dieser Methode, indem man mit Hilfe von Cepheidensternen die Distanz zu möglichst vielen Galaxien feststellt, in denen Typ Ia Supernovae registriert wurden. Die Supernova-Methode ist auch vielversprechend, weil sie theoretisch überzeugend begründet werden kann. Berücksichtigt man noch eine empirische Beziehung zwischen der Leuchtkraft im Maximum und dem zeitlichen Verlauf der Lichtkurve, kann die Hubble-Relation sehr genau bestimmt werden. Es wird sogar vermutet, daß bei Supernovae hoher Rotverschiebung die Abweichungen vom linearen Hubble-Gesetz zu sehen sind, wie sie in den FL-Modellen erwartet werden. Messungen mit dieser Methode führen auf Werte von

km s^-1 Mpc^-1, wobei

den systematischen Fehler abschätzt.

5 Das Weltalter t₀

Die ältesten Sterne befinden sich in den Kugelsternhaufen, die dicht gepackt 10⁵ bis 10⁷ Sterne enthalten und die unsere Milchstraße in einem sphärischen Halo umgeben. Die Altersbestimmung der Kugelsternhaufen ist eine interessante Mischung aus astronomischen Beobachtungen und Anwendungen der Sternentwicklungstheorie (Kugelsternhaufen). Die Unsicherheiten der verwendeten Sternmodelle liegen in der Beschreibung der Konvektion der Gasströmungen im Sterninneren, in den Opazitäten der äußeren Schichten des Sterns und den Anfangsverteilungen der chemischen Elemente. Die konsistente Verwendung neuer Zustandsgleichungen und Opazitäten führt zu einer Reduktion der bisherigen Schätzungen von (

) Milliarden Jahren auf (

) Milliarden Jahre. Dieser Wert stellt eine untere Grenze für t₀ dar. Zur Ermittlung der Entstehungszeit der ältesten Sterne rechnet man etwa 1 Milliarde Jahre hinzu. Insgesamt ergäbe sich somit ein Weltalter von

Jahre.

Für das Produkt

ergeben sich damit die Grenzen

; der Mittelwert (

) ist

. In Abb. 3 sind die beschriebenen Kurven in Abhängigkeit von

und

dargestellt. Für Modelle mit

und

, die aus theoretischen überlegungen favorisiert werden, ist

. Dieses Modell liegt nahe an der unteren Schranke, kann aber gegenwärtig auch noch nicht ausgeschlossen werden.

Aus Abb. 3 ist klar zu ersehen, daß auch für den Mittelwert

noch ein weiterer Bereich von FL-Modellen möglich ist.

6 Ω₀ und Ω_Λ

Die mittlere Dichte der Materie,

, ist eine wichtige Größe, aber ihr Wert ist nicht sehr genau bekannt. Die Standardmethode zur Messung von

geht aus von einer Zählung leuchtender Objekte. Die grundlegende Annahme ist dabei, daß im gesamten Universum das gleiche Verhältnis M / L aus Masse und Leuchtkraft gilt wie für die vermessenen Objekte. Für das Sternenlicht im Optischen gilt etwa

, was einem

entspricht. Dies ist natürlich nur eine untere Grenze, denn schon die Rotationsgeschwindigkeiten in den Galaxien zeigen an, daß es eine nichtleuchtende Materiekomponente gibt, die sich viel weiter erstreckt als das sichtbare Licht. Dies führt auf Abschätzungen von

und damit

. Mit verschiedenen Untersuchungsmethoden in Galaxienhaufen (Virialsatz, Röntgenemission, Gravitationslinsen) erhält man noch höhere

-Werte zwischen 100h und 400h.

dürfte demnach wohl zwischen 0,1 und 0,3 liegen. Die Fehler in diesen Methoden sind schwer abzuschätzen. Eine vernünftige Wahl ist vielleicht

. Vergleicht man diese Resultate mit den Grenzen für die kosmische Materie in baryonischer Form

, die man aus den Häufigkeiten der leichten Elemente Helium und Deuterium und deren Vorhersage aus Nukleosyntheserechnungen im Urknall ableitet,

, so kann man folgenden Schluß ziehen: Zwar gibt es auch nicht-leuchtende baryonische Materie, überwiegend liegt die dunkle Materie (DM) jedoch in nicht-baryonischer Form vor. Woraus könnte die nicht-baryonische DM bestehen? Mit ihrer kleinen Masse sind Neutrinos offensichtlich Kandidaten. Sie entstanden im frühen Universum ähnlich häufig wie Photonen, und gegenwärtig wird eine Neutrinodichte von einigen 100 pro cm³ geschätzt. Die Registrierung der Sonnenneutrinos im japanischen Experiment Super-Kamiokande erlaubt mit ziemlicher Sicherheit die Deutung, daß Neutrinos eine kleine Masse haben, allerdings wohl zu klein (nur etwa 10^-7 der Elektronenmasse), um kosmische Bedeutung zu erlangen. Für Strukturbildung im Kosmos können die Neutrinos ebenfalls nicht allein verantwortlich sein, denn sie können nicht im Halo von Galaxien eingefangen sein. Deshalb gibt es Vorschläge, die Halos der Galaxien aus schweren, schwach wechselwirkenden Teilchen aufzubauen. Kondensate aus Axionen, leichte, supersymmetrische Teilchen (Supersymmetrie) oder auch hypothetische Bindungszustände aus Gluonen existieren als theoretische Möglichkeiten, aber noch keiner dieser Kandidaten wurde experimentell gefunden.

Allein die Statistik der Gravitationslinsen gibt bis jetzt neben den Supernova-Beobachtungen eine Grenze für

:

7 Die Bildung leichter Atomkerne

Wenn die Temperatur der Urmaterie knapp unter hundert Millionen Grad liegt, also etwa 10^-4 Sekunden nach dem Urknall (dies ergibt sich, wenn man von der jetzt herrschenden Temperatur von 3 K ausgehend 15 Milliarden Jahre zurückrechnet), können wir noch gesicherte kernphysikalische Kenntnisse anwenden. Zu dieser Zeit hatten sich Protonen und Neutronen gebildet. Ungefähr 10 Sekunden später war die Temperatur so weit gefallen, daß auch Elektronen als stabile Teilchen existieren konnten. Anschließend wurden für einige Minuten verschiedene leichte Atomkerne gebildet, jedoch durch die Strahlung sofort wieder zerstört. Erst nach weiterer Abkühlung konnten die Elemente Deuterium und Helium überdauern, und es bildeten sich Helium- und Wasserstoffkerne (= Protonen) etwa im Verhältnis eins zu zehn. Das ist die heutzutage beobachtete Verteilung dieser Elemente. Alle schweren Elemente können in ausreichendem Maße in Sternen produziert werden, nur die leichten Elemente Deuterium und Helium nicht. Es ist sehr ermutigend, daß die kosmologischen Standardmodelle das quantitativ richtige Ergebnis liefern.

8 Strukturbildung

Die kosmologischen Urknall-Modelle haben sich hervorragend bewährt und für die kosmische Entwicklung etwa 1 Sekunde nach dem Urknall bis jetzt eine konsistente Beschreibung des Universums ermöglicht. Das Hauptproblem der Standardmodelle ist augenblicklich die Strukturentstehung in der kosmischen Materie: Was ist die Natur der Dunklen Materie? Wie sind die anfänglichen Schwankungen der Dichte entstanden? An diesen Fragen wird intensiv gearbeitet. Es könnte gut sein, daß eine endgültige Antwort nur in einer genauen Analyse von Quantenprozessen im frühesten Universum gefunden werden kann. Dies hängt mit dem grundsätzlichen, ungelösten Problem zusammen, eine umfassende Theorie zu finden, die als Grenzfälle sowohl die Quantentheorie wie auch die Allgemeine Relativitätstheorie enthält. Die frühesten Epochen des Universums und sein singulärer Anfang können wohl nur im Rahmen einer derartigen Theorie untersucht werden (Urknall).

Falls Galaxien der Hubbleschen Beziehung folgen, kann ihre Entfernung aus der Messung der Rotverschiebung erschlossen werden. Durch die Vermessung vieler Galaxien läßt sich so ein Bild von der räumlichen Verteilung der kosmischen Materie auf großen Skalen gewinnen. Große Rotverschiebungskataloge, die in den letzten Jahren erstellt wurden und die einige 10 000 Galaxien enthalten, enthüllen eine Vielfalt interessanter Strukturen. Die Galaxien sind in Filamenten und dünnen Schichten konzentriert, die große nahezu kugelförmige Leerräume (›voids‹ mit typischen Dimensionen von 20 bis 50 Mpc) umschließen. Diese für das Auge klar erkennbare Zellstruktur konnte bis jetzt noch nicht quantitativ durch geeignete statistische Größen erfaßt werden.

Die modernen kosmologischen Theorien gehen davon aus, daß diese Strukturen sich aus anfänglich kleinen Schwankungen einer gleichförmigen Hintergrunddichte entwickelt haben, allein durch die Wirkung der Schwerkraft. Der Dichtekontrast

(

: gleichförmige Hintergrunddichte), wächst wegen der kosmischen Expansion, die das normale, exponentielle Anwachsen der Gravitationsintabilität aufzehrt, wie eine Potenz der Zeit an:

, oder äquivalent

, im Modell mit

.

In baryonischer Materie kann der Dichtekontrast erst nach der Rekombinationszeit anwachsen, wenn Strahlung und Materie entkoppelt sind. Dies begrenzt den Anwachsfaktor auf

(z_R: Rotverschiebung der Rekombinationsepoche) für

.

Für

ist die Anwachsrate kleiner. Auch die Tatsache, daß die ersten Galaxien bereits bei z = 5,6 entdeckt wurden, deutet darauf hin, daß der realistische Anwachsfaktor deutlich kleiner als (1 + z_R) sein dürfte. Die Anfangsamplitude wird aber im plausiblen Fall konstanter Entropie

begrenzt durch die COBE-Messungen der Strahlungsanisotropie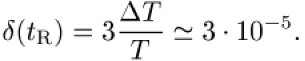

Dann wäre

bis heute nur auf etwa 5 · 10^-2 angewachsen, d.h. Galaxien und Galaxienhaufen hätten sich noch nicht bilden können. Die Anisotropien im Mikrowellen-Hintergrund schließen also ein Universum mit rein baryonischer Materie aus. Darin könnten sich die beobachteten Strukturen nicht bilden. Deshalb postuliert man die Existenz dunkler, nichtbaryonischer Materie (DM), was ja auch durch die Messungen der Dichte nahegelegt wird.

Dichtefluktuationen der Materie wachsen an, sobald die Materiedichte die Energiedichte der Strahlung überwiegt. Zusätzlich vorhandene DM verlegt diesen Zeitpunkt zu höheren Rotverschiebungen (etwa um den Faktor 10), gibt also den Dichteschwankungen mehr Zeit zum Anwachsen. Nichtbaryonische DM koppelt außerdem nicht direkt an das Strahlungsfeld. Deshalb erscheinen ihre Schwankungen im Mikrowellen-Hintergrund nur aufgrund des tieferen Gravitationspotentials, das die Photonen durchlaufen müssen. Dies sind zwei entscheidende Vorteile der nichtbaryonischen DM. Nach der Rekombination fallen die Baryonen ins Schwerepotential der DM und bilden schließlich Galaxien und erste Sterne.

Jedes theoretische Modell der Strukturbildung erfordert eine Reihe von Zutaten: Die Amplituden und das Spektrum der anfänglichen Dichteschwankungen sowie die Zusammensetzung der DM sind nötig, um ein Modell festzulegen, dessen Entwicklung numerisch verfolgt werden kann. Zusätzlich müssen natürlich die Parameter des kosmologischen Modells

eingegeben werden. Die numerischen Simulationen sind eigentlich nichts weiter als die Integration der Newtonschen Bewegungsgleichungen (Newtonsche Mechanik) für N Teilchen, die nur durch die Gravitation in Wechselwirkung stehen. Im Augenblick kann man die Entwicklung von 10⁷ Teilchen im Simulationsvolumen verfolgen, bis zur Entstehung stark geklumpter Dichtekonzentrationen. Dies entspricht i.a. einer Auflösung bis zur Massenskala von Galaxien. Allerdings wird nur die DM auf diese Weise verfolgt, die Kondensation der Baryonen sowie die physikalischen Heizungs- und Kühlungsprozesse bei der Galaxienbildung sind noch nicht in diese Rechnungen integriert.

Der Vergleich der DM Modelle mit der beobachteten Galaxienverteilung zeigt, daß die ›Pseudo-Galaxien‹ der Modelle die Maxima der Dichteverteilung etwas anders verteilt sind als die ›echten‹ Galaxien. Man muß einen ›bias‹-Faktor einführen, um die DM-Modelle mit den Beobachtungen in Einklang bringen zu können. Letzten Endes kann es natürlich nur ein korrektes Modell der Strukturbildung geben, da die kosmischen Parameter, ebenso wie der Anteil und die Art der DM, aus Beobachtungen bestimmt werden sollten. Das Anfangsspektrum der Dichtestörungen und der ›bias‹-Faktor sollten aus physikalischen Prozessen im frühen Universum, bzw. bei der Galaxienbildung, berechenbar sein.
Literatur:
G. Börner: The Early Universe, dritte Auflage, Springer, 1993.
J.A. Peacock: Cosmological Physics, Cambridge UP, 1999.

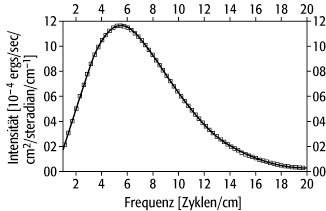
Kosmologie 1: Spektrum der kosmischen Mikrowellenstrahlung, vermessen vom NASA-Satelliten COBE. Die Kästchen sind die Messungen mit ihren Fehlern, die durchgezogene Kurve entspricht einem Planck-Spektrum der Temperatur T = 2,73 K. Aufgetragen ist die Intensität gegen die Wellenzahl.

Kosmologie 2: Expansionsfaktor

als Funktion der kosmischen Zeit t.

kennzeichet

-Kurven mit

; die Kurve mit

illustriert den Einfluß einer positiven kosmologischen Konstanten.

Kosmologie 3: Linien konstanter Werte von

in Abhängigkeit von

und

.