Anthropologie: Auf ganzer Linie
Lässt sich etwas verstehen, wofür es keine Worte gibt? Eine umstrittene Frage, für die Linguisten gerne nach Amazonien reisen. Denn hier leben Völker, an denen etliche Errungenschaften der westlichen Zivilisation vorbeigegangen sind. Geometrie zum Beispiel.

© Science (Ausschnitt)
Sokrates: Hat er sie nun immer gehabt, so ist er auch immer wissend gewesen.
Hat er sie aber einmal erlangt, so hat er sie wenigstens nicht in diesem Leben erlangt.
Oder hat jemand diesen die Geometrie gelehrt?
Denn gewiss wird er mit der ganzen Geometrie ebenso verfahren und mit allen andern Wissenschaften auch.
Hat nun jemand diesen dies alles gelehrt?
Denn du musst es ja wohl wissen, da er in deinem Hause geboren und erzogen ist.
Menon: Ich weiß sehr gut, dass niemand sie ihn jemals gelehrt hat.
Sokrates: Er hat aber diese Vorstellungen – oder nicht?
Menon: Notwendig, wie man ja sieht.
Ein kleines Experiment genügte Sokrates, um zu demonstrieren, dass jeder Mensch über ein gewisses Grundwissen verfügt. Im Dialog mit Menon – überliefert um 390 v. Chr. von seinem Schüler Platon – lässt er einen Sklavenjungen, der noch nie etwas über Mathematik gehört hat, durch geschickte Fragen zu geometrischen Einsichten gelangen.
Sind geometrische Kenntnisse damit angeboren? Können wir Geometrie verstehen, auch wenn wir keine Begriffe für "Punkt", "Gerade", "Winkel" oder "Dreieck" haben? Wer sich nur mit Grausen an den Mathematik-Unterricht in der Schule erinnert, mag kaum daran glauben. Und auch manche Linguisten äußern hier Zweifel.
Wie einst Benjamin Lee Whorf und Edward Sapir. Die beiden Wissenschaftler waren fest davon überzeugt, dass die Sprache unser Denken fundamental beeinflusst: Wofür die Sprache keinen Begriff hat, bleibt – im wahrsten Sinne des Wortes – undenkbar. Wem also noch nie in seinem Leben Dreiecke über den Weg gelaufen sind, dem sollte die geometrische Idee dahinter unverständlich bleiben.
Seit Euklid ist es allerdings schwierig, Menschen zu finden, die keine Ahnung von Geometrie haben. Es sei denn, man reist nach Brasilien in die amazonischen Wälder. Hier leben tatsächlich noch Völker, die ohne mathematische Begriffe auskommen – und sich damit zunehmender Beliebtheit für Psychologen und Sprachwissenschaftler erfreuen.
Und so begab sich auch Pierre Pica von der Universität Paris ins ferne Amazonien an den Fluss Cururu zu den Stamm der Mundurukú, um dort im Auftrag seiner Kollegen Stanislas Dehaene und Véronique Izard vom französischem Forschungsverbund Inserm sowie Elizabeth Spelke von der amerikanischen Harvard-Universität geometrische Studien durchzuführen.
© Science (Ausschnitt)
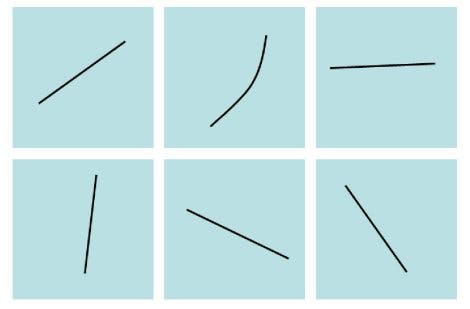
Linien | Eine leichte Aufgabe: Aus sechs Linien ist die "seltsame" oder "hässliche" zu finden. Obwohl sie keinen Begriff für "Gerade" haben, wählten 93 Prozent der Mundurukú korrekt die gekrümmte Linie (oben Mitte).
© Science (Ausschnitt)
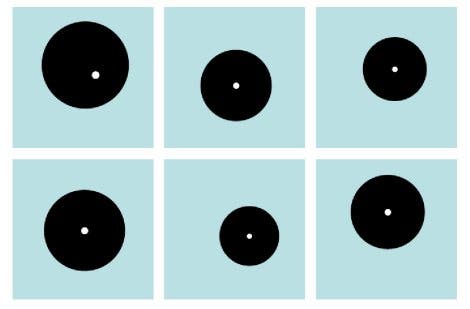
Kreise | Hier fällt eine Kreis-Figur aus der Reihe. 68 Prozent der Versuchspersonen aus Amazonien erkannten den Kreismittelpunkt (oben links) als entscheidendes Kriterium.

© Science (Ausschnitt)
Dreiecke | Hier wird es schon schwieriger. Welche Figur passt nicht?
43 Prozent der Mundurukú wussten es: Die Anordnung unten rechts ist nicht punkt-symmetrisch.
43 Prozent der Mundurukú wussten es: Die Anordnung unten rechts ist nicht punkt-symmetrisch.
Auch das lösten die Mundurukú mit Bravour. Zu 71 Prozent konnte Jung und Alt die in der Karte verschlüsselte Information richtig deuten. Die Trefferquote lag damit wiederum genauso hoch wie bei Kindern aus den fernen USA, aber niedriger als bei US-amerikanischen Erwachsenen.
Demnach gibt es wohl tatsächlich ein gewisses geometrisches Grundverständnis, das allerdings – wie die Probanden aus den USA zeigten – durch Erziehung und Erfahrung verbessert werden kann. Der Gebrauch von Karten, ein vernünftiger Mathematik-Unterricht, aber auch geometrische Begriffe in der Sprache fördern erheblich geometrisches Denken.
"Aber das spontane Verständnis geometrischer Konzepte und Karten dieser abgeschiedenen menschlichen Gesellschaft zeigt", so schließen die Wissenschaftler, "dass ein geometrisches Kernwissen, wie arithmetische Grundkenntnisse, zum universellen Bestandteil des menschlichen Geistes gehört."
Sokrates wusste das schon vor 2400 Jahren.




Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.