Der erste Schritt auf der Reise in höhere Dimensionen ist wortwörtlich ein Kinderspiel. Schneiden Sie aus farbigem Papier ein paar Rauten mit dem Öffnungswinkel 60 Grad aus, in drei verschiedenen Farben. Die Vorlage dazu finden Sie hier:

Dann bitten Sie etwaige Kinder (oder sich selbst), mit diesen Rauten die Tischplatte lückenlos und ohne Überdeckung zu belegen. Die einzige Vorschrift dazu lautet, dass die gelben Rauten stehend , die blauen aufsteigend und die roten absteigend zu legen sind.

Es dauert nicht lange, dann springt einem eine räumliche Struktur ins Auge: je nachdem, wie sorgfältig die Kinder gelegt haben, ein mehr oder weniger ordentlicher Stapel aus lauter Würfeln.

Es ist sogar möglich, aus diesem gedachten Stapel einen Würfel wegzunehmen oder hinzuzufügen, indem man ein Sechseck aus drei verschiedenfarbigen Rauten 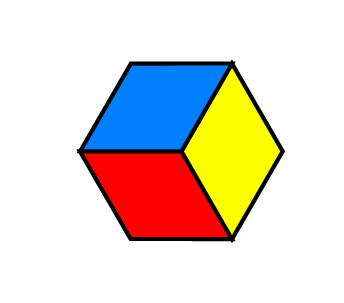herausnimmt und umgedreht wieder einsetzt .

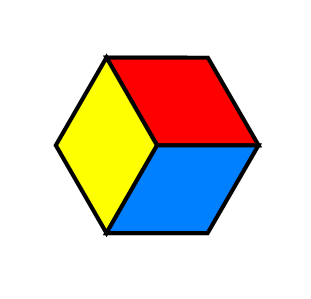Der gedachte Würfel steht auf einer Ecke, seine gegenüberliegende Ecke ist genau vertikal darüber, und wir betrachten das Ganze exakt von oben: eine Parallelprojektion. Das gilt ebenso für alle anderen Würfel des Stapels. Von oben sehen wir nur die drei Flächen, die der obersten Ecke anliegen; nimmt man sie weg, so kommen die drei anderen Flächen des Würfels zum Vorschein.

Man könnte natürlich nur eine oder zwei der drei Flächen wegnehmen; aber dann sieht man die darunterliegenden Flächen nur zum Teil, was wir im Folgenden vermeiden wollen. Nicht nur, weil das nicht so schön regelmäßig aussieht, sondern auch, weil die Sache in höheren Dimensionen ziemlich unübersichtlich wird.

Parallelprojektion von einem n-dimensionalen Raum in die zweidimensionale Ebene funktioniert nämlich nicht nur, wenn wir uns in unserem vertrauten Raum mit n = 3 befinden. Aber da es in höheren Dimensionen mit dem Vorstellungsvermögen etwas hapert, müssen wir die abstrakte Vektorschreibweise zu Hilfe nehmen.

Der Bequemlichkeit halber setzen wir eine Ecke unseres Würfels in den Nullpunkt des Koordinatensystems und lassen die Kanten, die von dieser Ecke ausgehen, entlang der Koordinatenachsen verlaufen.

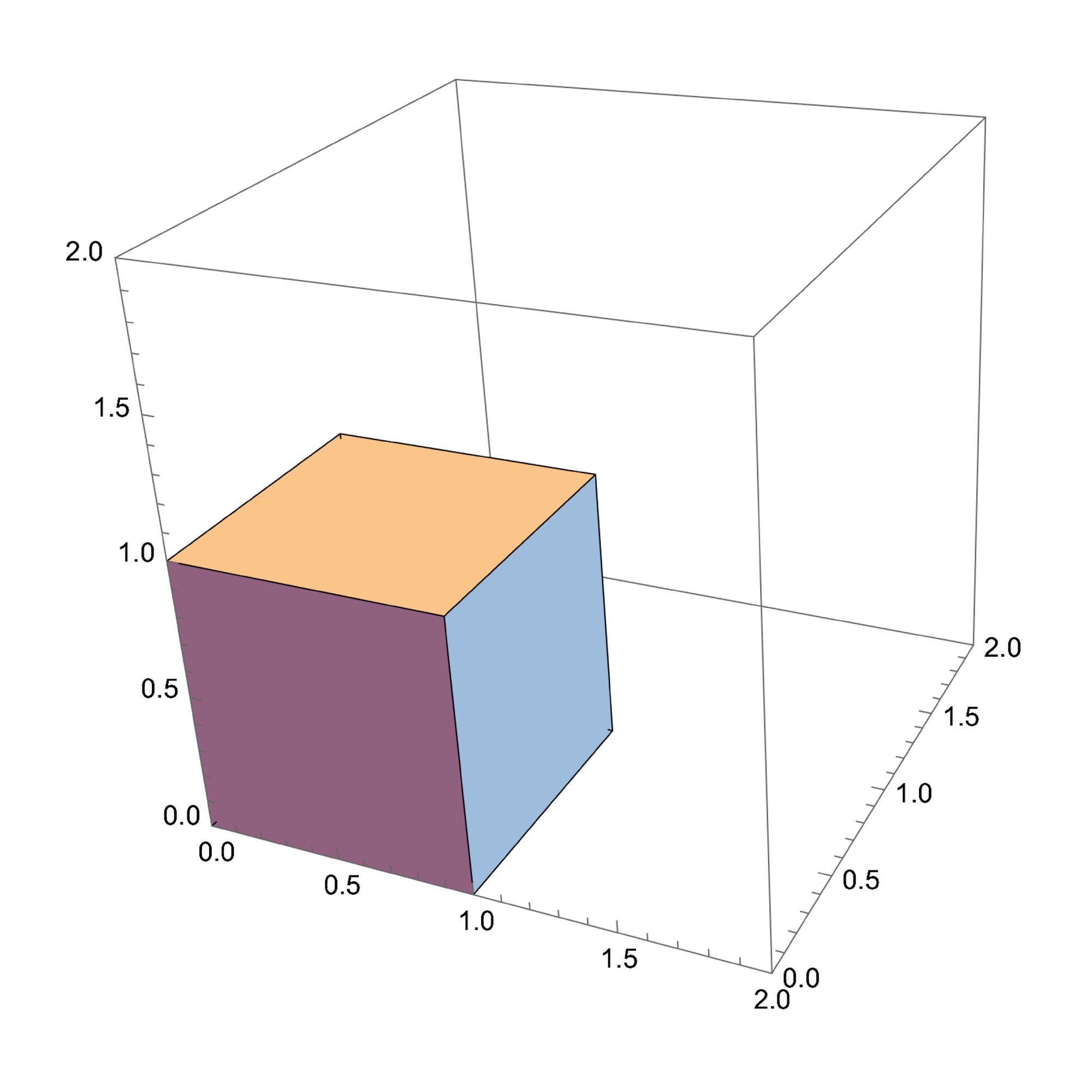
Und da es auf die Länge der Kanten nicht wirklich ankommt, setzen wir sie gleich 1. Dann hat in unserem dreidimensionalen Raum dieser Würfel (der »Einheitswürfel«) die Ecken mit den Koordinaten (0, 0, 0), (0, 0, 1), (0, 1, 0), …, (1, 1, 1): alle möglichen Kombinationen der Werte 0 und 1. Das ist im allgemeinen Fall nicht wesentlich anders. Im n-dimensionalen Raum ist jeder Punkt eine Folge von n reellen Zahlen (ein Vektor). Der n-dimensionale Einheitswürfel hat 2ⁿ Ecken, und jede Ecke ist ein Vektor mit n Komponenten, die entweder 0 oder 1 sind.

Während ein gewöhnlicher Würfel (n = 3) von sechs Flächen (n = 2) begrenzt wird, sind die »Grenzflächen« eines n-dimensionalen Würfels (n−1)-dimensionale Würfel, die ihrerseits von (n−2)-dimensionalen Würfeln begrenzt werden, bis hinunter zu dreidimensionalen Grenzwürfeln und den Flächen (n = 2), Kanten (n = 1) und Ecken (n = 0), die uns aus dem gewöhnlichen Raum geläufig sind.

Um einen solchen Einheitswürfel auf die Ebene zu projizieren, stellen wir ihn wieder auf die Ecke (0, 0, …, 0) und positionieren ihn so, dass die gegenüberliegende Ecke (1, 1, …, 1) genau vertikal darüber liegt. Nur ist in mehr als drei Dimensionen nicht klar, was eigentlich »vertikal darüber« heißen soll. In der Tat gibt es viel mehr Möglichkeiten zu projizieren, als man sich vorstellen kann. Aber der Einfachheit und der Symmetrie zuliebe legen wir uns auf Folgendes fest: Die Ecken, die dem Nullpunkt benachbart sind (die n »Einheitsvektoren«), sollen auf Punkte in der Ebene abgebildet werden, die in gleichen Abständen auf dem Umfang eines Kreises liegen, insbesondere also alle den gleichen Abstand vom Nullpunkt haben.

Für n = 3 ergibt diese Projektion das oben beschriebene Sechseck aus drei Rauten. Für höhere Dimensionen werden nicht nur die n Seitenflächen, die an den Punkt (1, 1, …, 1) angrenzen, sichtbar, sondern deutlich mehr.

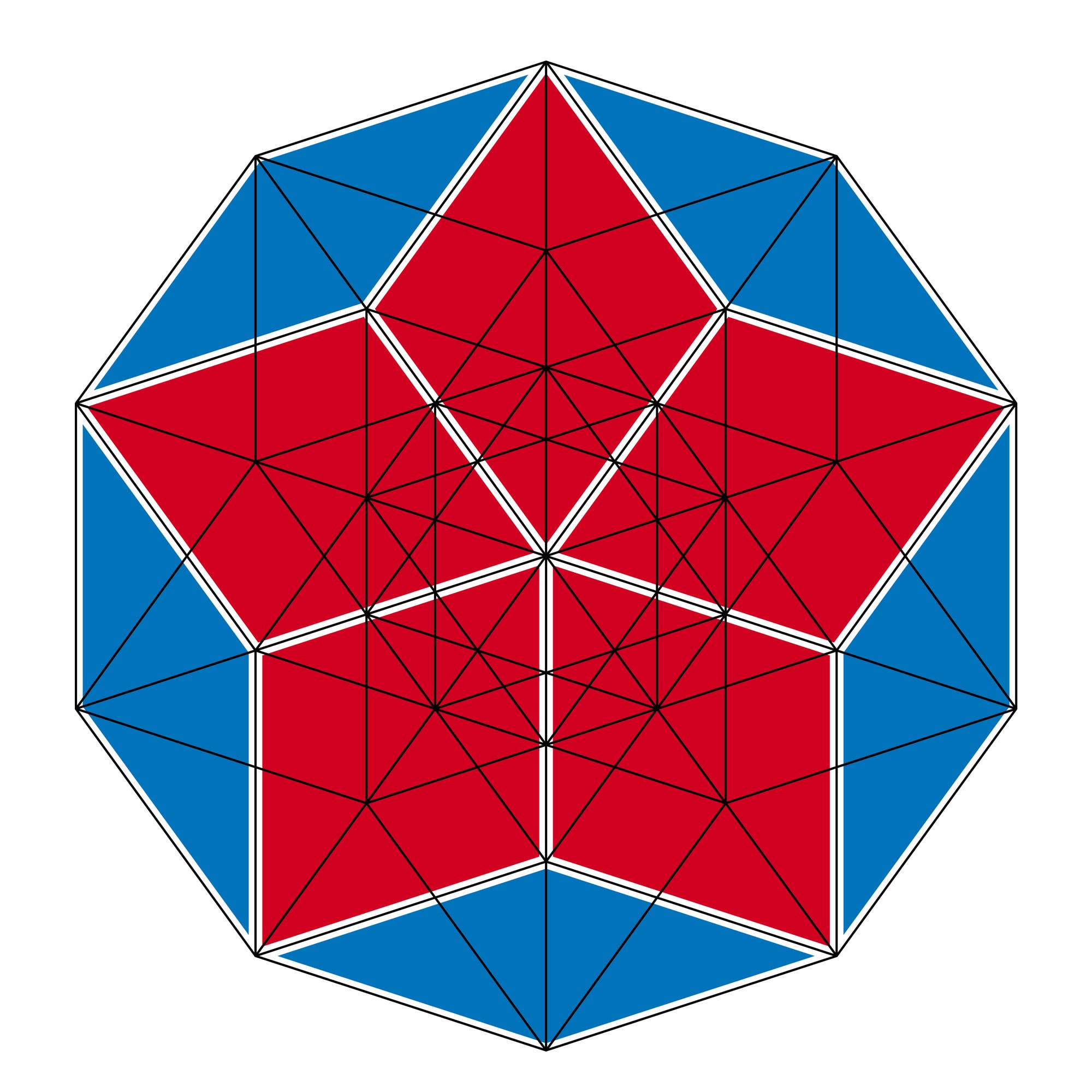
Die äußere Begrenzung des Projektionsbilds ist in jedem Fall ein regelmäßiges (2n)-Eck. Dessen Inneres füllen lückenlos allerlei Rauten, die sämtlich perspektivisch verzerrte Bilder von Quadraten sind – zweidimensionalen Seitenflächen des hochdimensionalen Würfels. Es sind diejenigen, die »in Blickrichtung zuoberst« liegen, was immer das in hohen Dimensionen heißen mag.

Zwei verschiedene Einheitsvektoren stehen stets senkrecht aufeinander. Das ist die Stelle, an der in mehr als drei Dimensionen unser Vorstellungsvermögen aussetzt. Aus dem rechten Winkel zwischen Einheitsvektoren wird in der Projektion der Winkel zwischen den entsprechenden Punkten auf dem Kreisumfang, und da ist die Auswahl nicht besonders groß. Für ungerade n gibt es nicht mehr als (n−1)/2 verschiedene Rauten.

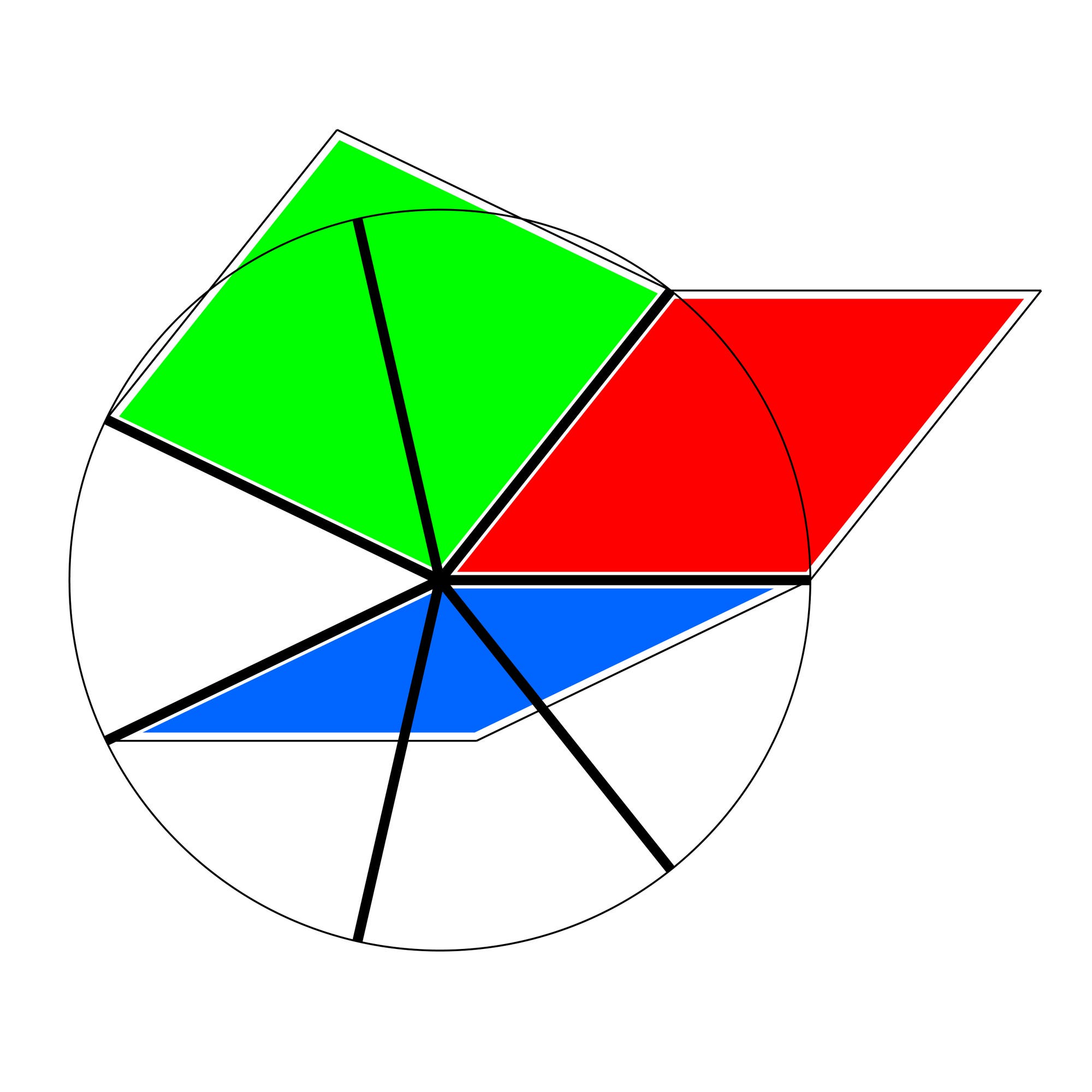
Auch im n-dimensionalen Fall kann man drei Quadrate, die einem Eckpunkt anliegen, wegnehmen, woraufhin drei andere Quadrate zum Vorschein kommen, die gemeinsam mit den weggenommenen einen dreidimensionalen Grenzwürfel bilden. Allerdings ist dieser Würfel nur einer von zahlreichen, die der Ecke anliegen. Dem entspricht im Projektionsbild die Aktion, ein Sechseck aus drei aneinandergrenzenden Rauten aus dem Bild herauszunehmen und umzudrehen.

Damit sind die Möglichkeiten, Grenzwürfel wegzunehmen, noch nicht erschöpft. Im Projektionsbild tun sich neue Sechsecke auf, die ihrerseits umgedreht werden können, wodurch wieder andere Füllungen des (2n)-Ecks mit denselben Rauten entstehen. Heinz Klaus Strick, Mathematiker und ehemaliger Leiter eines Gymnasiums in Leverkusen, hat vor Jahren mit seinen Schülern ein hübsches Spiel daraus gemacht.

Dreidimensionale Schatten des Einheitswürfels

Eigentlich müssen wir uns beim Projizieren nicht auf die zwei Dimensionen der Ebene beschränken. Schließlich haben wir noch eine dritte Dimension zur Verfügung. Dafür ist das bisher angewandte Prinzip »Bilde die Einheitsvektoren auf gleichmäßig verteilte Punkte auf dem Kreisumfang ab« nur geringfügig abzuändern: Man erhebt den Kreis ein Stück über die (x, y)-Ebene hinaus. Dann stehen die Rauten, die an den Nullpunkt grenzen, schräg nach oben. Der nächste Kranz an Rauten, der wie im zweidimensionalen Fall durch den ersten bestimmt ist, steht schon etwas steiler, die dritte noch etwas mehr, bis schließlich eine Reihe vertikal angeordnet oder sogar nach innen geneigt ist. Ab da schließt sich das Gebilde, bis sich die Rauten eines Kranzes wieder in einem Punkt treffen. Das ist das Bild der fernsten Ecke des n-dimensionalen Einheitswürfels, des Punkts mit den Koordinaten (1, 1, …, 1). So entstehen die so genannten »polaren Zonoeder«, die ich in einem anderen Artikel als »Zwiebelkörper« bezeichnet habe.

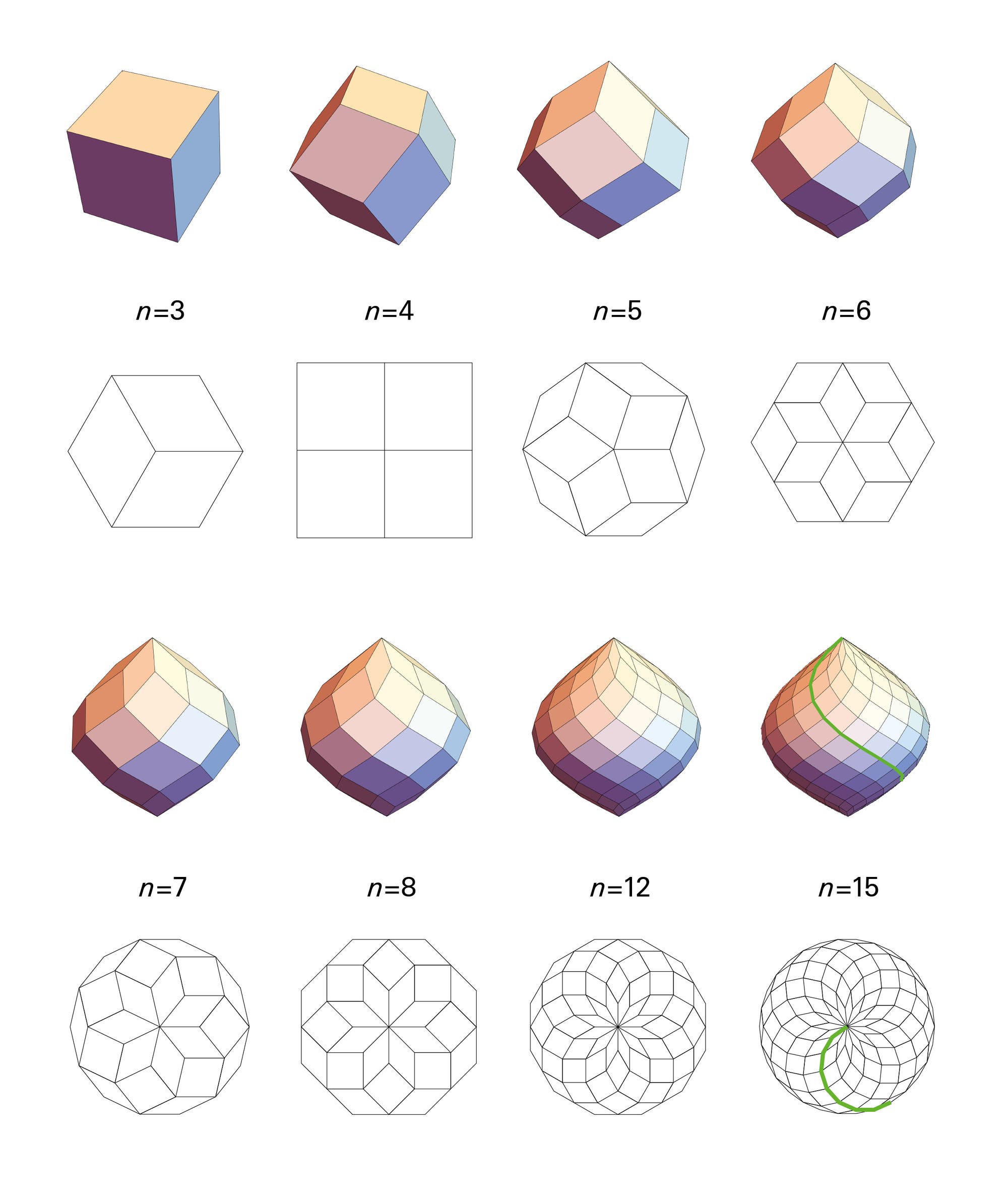
Sie heißen polar, weil sie zwei prominente »Pole« haben, an denen sich jeweils n Rauten treffen; alle anderen Ecken sind nur Treffpunkte von drei oder vier Rauten. Zonoeder heißen sie, weil sie aus lauter »Gürteln« bestehen (Zone ist das altgriechische Wort für Gürtel). Gemeint sind Folgen von rautenförmigen Seitenflächen, bei denen jede Raute über zwei nicht benachbarte – und damit parallele – Seitenflächen mit ihrer Nachbarin verbunden ist. Bei diesen Zonoedern kreuzen sich in jeder Raute sogar zwei Gürtel, und der ganze Körper ist spiegelsymmetrisch. Alle Gürtel verlaufen spiralförmig von Pol zu Pol. Zu allem Überfluss ist ein Zonoeder rotationssymmetrisch bezüglich der Achse, die durch beide Pole verläuft: Dreht man es um den n-ten Teil des Vollwinkels, sieht es wieder genau so aus wie zuvor.

Die rundliche Form und das einfache Bildungsgesetz haben verschiedene Architekten dazu motiviert, Gebäude in der Form polarer Zonoeder zu errichten, vom Kinderhäuschen im Garten bis zum spektakulären Turm der Rückversicherungsgesellschaft Swiss Re in London. Aber unter der glatten Oberfläche verbirgt sich viel Struktur, und das umso mehr, je höher die Dimension ist. Schon das Kantenmodell des fünfdimensionalen Einheitswürfels sieht ziemlich unübersichtlich aus.

Insbesondere stecken im Inneren jedes polaren Zonoeders zahlreiche Rhomboeder, das sind perspektivisch verzerrte gewöhnliche (dreidimensionale) Würfel. Sie überlappen sich vielfach; so gehört jede Raute an der Oberfläche des Zonoeders zu n−2 verschiedenen Rhomboedern, denn nachdem die Raute selbst zwei Dimensionen in Anspruch nimmt, stehen für die dritte Dimension des Rhomboeders noch n−2 Richtungen zur Auswahl. Aber es herrscht nicht das totale Chaos. Man kann aus den vielen Rhomboedern eine Teilmenge auswählen, welche den ganzen Körper lückenlos und ohne Überlappungen ausfüllt; es gibt sogar verschiedene Teilmengen mit dieser Eigenschaft. Das entspricht – viele Dimensionen höher – der Tatsache, dass man das Projektionsbild des gewöhnlichen Würfels aus drei Rauten zusammensetzen kann. In dem Fall legt die erste Raute die übrigen fest. Im Gegensatz dazu bestimmt das erste Rhomboeder die Zerlegung des Zonoeders noch nicht vollständig, aber es schränkt die Möglichkeiten bereits ein.

Anfang der 1980er Jahre stieß Russell Towle aus der kalifornischen Kleinstadt Dutch Flat auf die Zonoeder – eine Begegnung, die sich zu einer jahrzehntelangen Besessenheit entwickelte. Auf der Suche nach einer Formel für das Volumen eines Zonoeders erkundete er Möglichkeiten, den ganzen Körper aus einer geeigneten Auswahl von Rhomboedern zusammenzusetzen, denn das Volumen eines solchen verzerrten Würfels ist relativ einfach zu berechnen. Das wiederum veranlasste ihn, die innere Struktur einer derartigen Zusammensetzung näher zu erkunden.

Von den zwölf Kanten jedes Rhomboeders sind wie beim unverzerrten Würfel jeweils vier untereinander parallel; es kommen also insgesamt nur drei verschiedene Richtungen vor, die ihrerseits parallel zu den Projektionsbildern von drei der n Einheitsvektoren sind. Im Inneren des Zonoeders kommen daher dieselben rautenförmigen Seitenflächen vor wie an der Oberfläche, und das Sortiment dieser Flächen ist ziemlich begrenzt. Deswegen treten sogar getreue Kopien von Teilen der Oberflächenstruktur zu Tage, wenn man eine geeignete Teilmenge an Rhomboedern wegnimmt.

Auf der Suche nach solchen Strukturen entdeckte Russell Towle eine merkwürdige neue Art von dreidimensionalem Körper. Wenn n nicht gerade eine Primzahl ist, sondern zusammengesetzt wie zum Beispiel 15 = 3·5, dann kann man das Zonoeder auf eine spezielle Weise zurechtstutzen. Von den 15 Spiralwegen von Pol zu Pol bleibt nur jeder fünfte stehen; alle anderen verschwinden, indem man nicht nur die an diese Spiralwege angrenzenden Rhomboeder wegnimmt, sondern darüber hinaus noch so viele, dass wieder eine glatt aussehende Teilfläche entsteht. Wenn allgemein n = m·k Produkt zweier Faktoren ist, die beide größer als 1 sind, dann kann man aus dem polaren Zonoeder der Größe n einen Körper herausschälen, der k (oder auch m) spiralförmige »Grate« und dazwischen vergleichsweise glatte Teilflächen hat, die der Oberfläche des Zonoeders zumindest teilweise ähnlich sehen. Towle hat diese Körper Spiraloeder (spirallohedra) genannt.

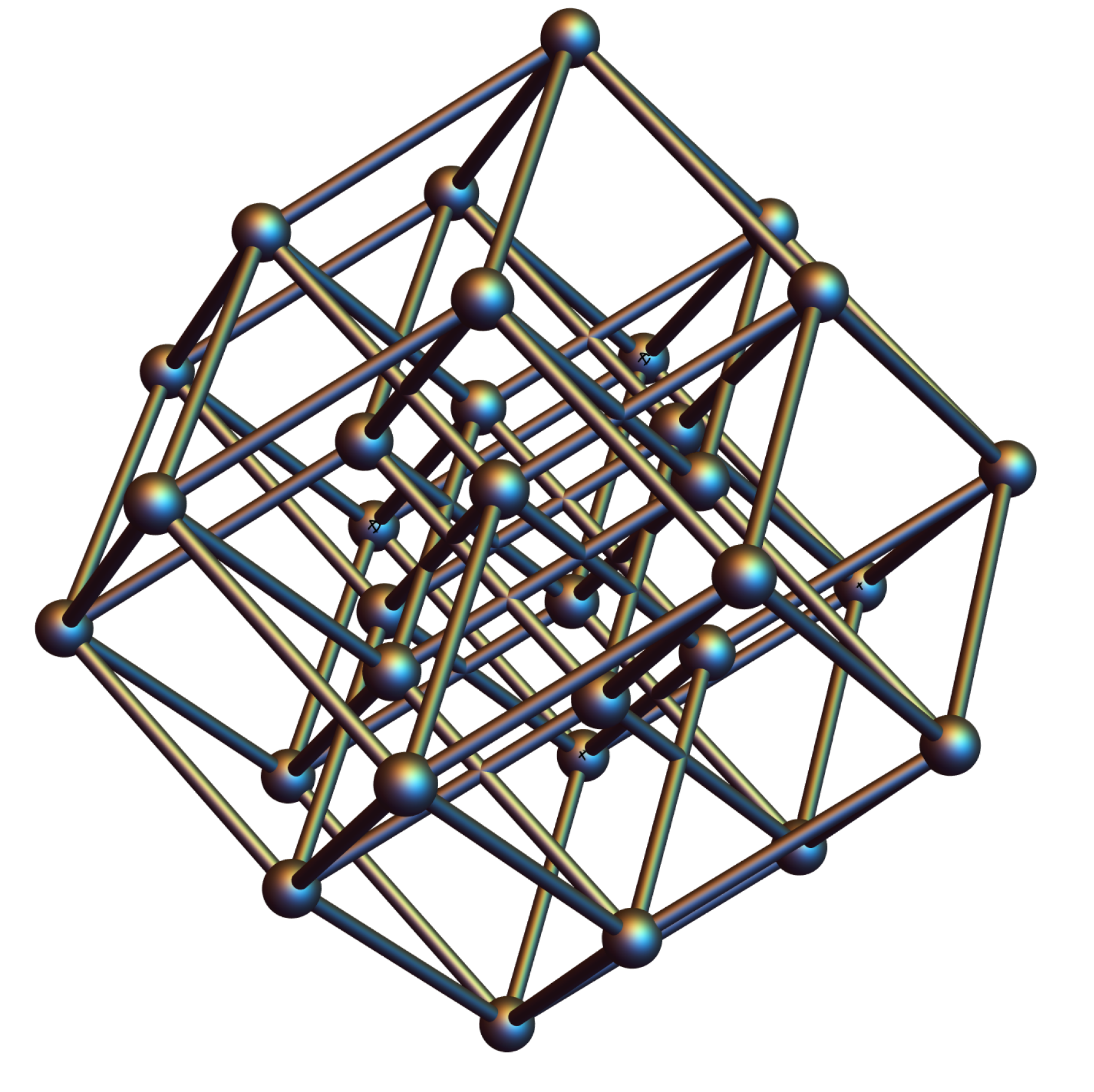
Sie sind interessant gebaut, haben aber offensichtlich weniger Symmetrien als ihr Ursprungskörper. Von der n-zähligen Symmetrie des Zonoeders ist nur noch eine k-zählige übrig geblieben, und die Spiegelsymmetrien sind gänzlich verschwunden. Dafür haben sie eine neue Eigenschaft, zumindest wenn k gleich 3, 4 oder 6 ist: Sie sind Raumfüller!

Man kann beliebig viele Exemplare dicht an dicht und lückenlos zusammenpacken. Dabei sind sie in allen drei Raumrichtungen periodisch angeordnet: Jedes Spiraloeder der Packung geht aus jedem anderen durch eine Parallelverschiebung (Translation) hervor. So erklärt sich auch die Beschränkung auf die Werte 3, 4 und 6: Legt man durch die Packung eine Ebene, in der zwei der drei Translationsvektoren liegen, wird daraus eine Pflasterung ebenjener Ebene mit lauter kongruenten Flächen, die durch Translation auseinander hervorgehen. Dann aber müssen diese Flächen so angeordnet sein wie die bekannte Dreiecks-, Quadrat- beziehungsweise Bienenwabenpflasterung der Ebene.

Towle hat sehr viel am Computer mit den Spiraloedern experimentiert. Und wenn er nicht 2008 bei einem Verkehrsunfall ums Leben gekommen wäre, hätte er zweifellos die bislang noch unvollständige Theorie solcher Körper weiter vorangetrieben.

Mittlerweile rühmen viele Fachkollegen sein Werk, aber bislang hat es niemand nennenswert weiterentwickelt. Mit einer Ausnahme: Bei den polaren Zonoedern kann man n gegen unendlich gehen lassen. Die zunächst sehr eckigen Körper werden dabei immer glatter, bis im Grenzfall ein perfekter Rotationskörper herauskommt. Dieser entsteht, wenn man den positiven Teil einer Sinuskurve, also den Abschnitt von 0 bis π, um die x-Achse rotiert. Frans Snik von der Universität Utrecht (Niederlande) hat denselben Grenzprozess, geeignet modifiziert, auf die Spiraloeder angewandt. Man hält dafür k fest und lässt n = km gegen unendlich gehen. Das Ergebnis ist ein perfekt glatter, von krummen Flächen begrenzter Körper mit k Graten, der für k = 3, 4 oder 6 ebenfalls ein Raumfüller ist.

Bastelanleitungen: