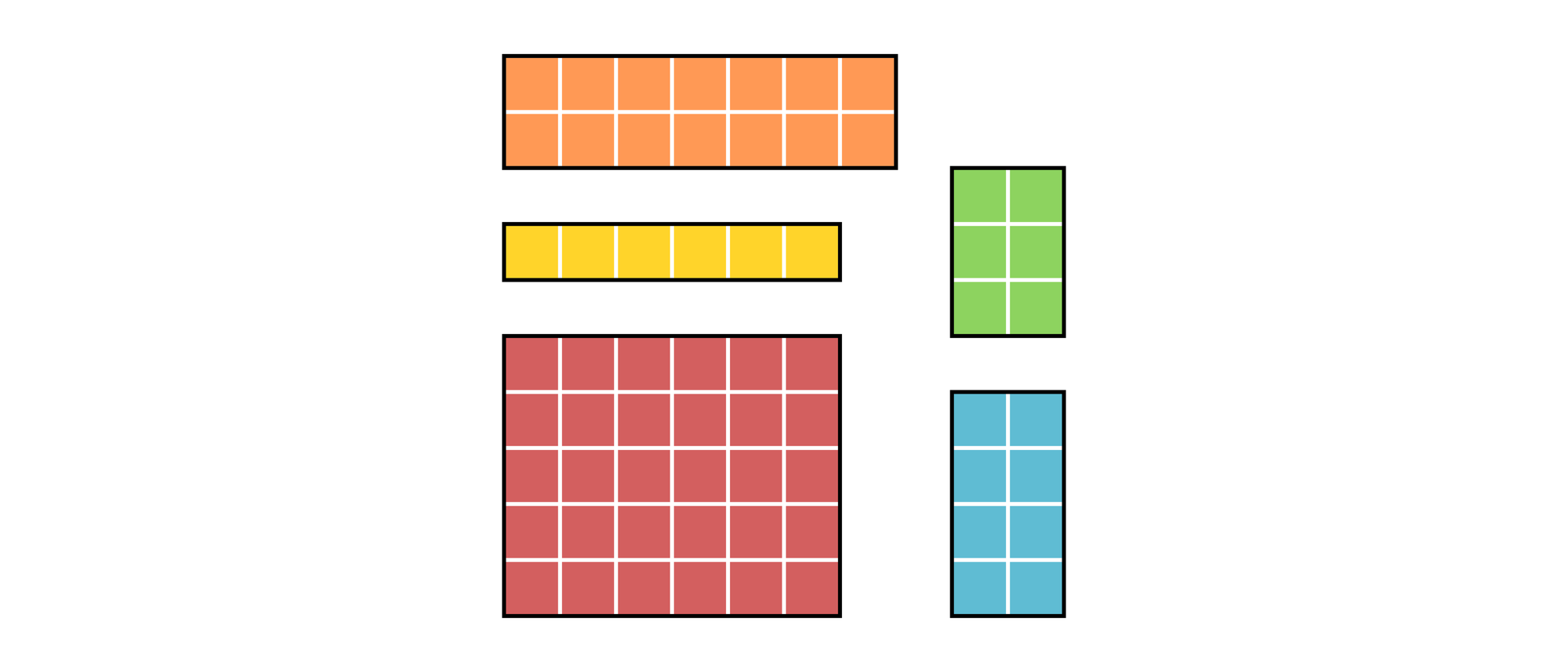
Hemmes mathematische Rätsel: Auf welche Weise kann hier ein Quadrat entstehen?
© Heinrich Hemme (Ausschnitt)
Ordnen Sie diese fünf Rechtecke, die aus lauter gleich großen Quadraten zusammengesetzt sind, zu einem Quadrat an. Dabei dürfen die Rechtecke sich nicht überlappen, nicht über den Rand des Quadrates ragen und keine Lücken in dem Quadrat frei lassen.
Die fünf Rechtecke bestehen aus 2×7 + 1×6 + 5×6 + 3×2 + 4×2 = 64 kleinen Quadraten. Haben die kleinen Quadrate die Seitenlänge 1, so sind die Seiten des großen Quadrates √64 = 8 lang. Das 2×7-Rechteck kann nur in dem großen Quadrat untergebracht werden, wenn seine kurze Seite mit der langen Seite des 1×6-Rechtecks zusammenstößt. Der Rest ist nun einfach. Bis auf Drehungen und Spiegelungen ist die Lösung eindeutig.
© Heinrich Hemme (Ausschnitt)
Schreiben Sie uns!
Beitrag schreiben