Hemmes mathematische Rätsel: Die Kondensatorleiter
In meinem 2008 erschienenen Buch »Düsentrieb contra Einstein« habe ich den Lesern erstmals das Problem der Kondensatorleiter gestellt. Kondensatoren sind Bauteile, die in fast jedem elektrischen Gerät stecken. Schaltet man mehrere Kondensatoren parallel, addieren sich ihre einzelnen Kapazitäten zur Gesamtkapazität C = C1 + C2 + C3 + …, schaltet man jedoch mehrere Kondensatoren in Reihe, addieren sich die Kehrwerte der Kapazitäten zum Kehrwert der Gesamtkapazität 1/C = 1/C1 + 1/C2 + 1/C3 + …
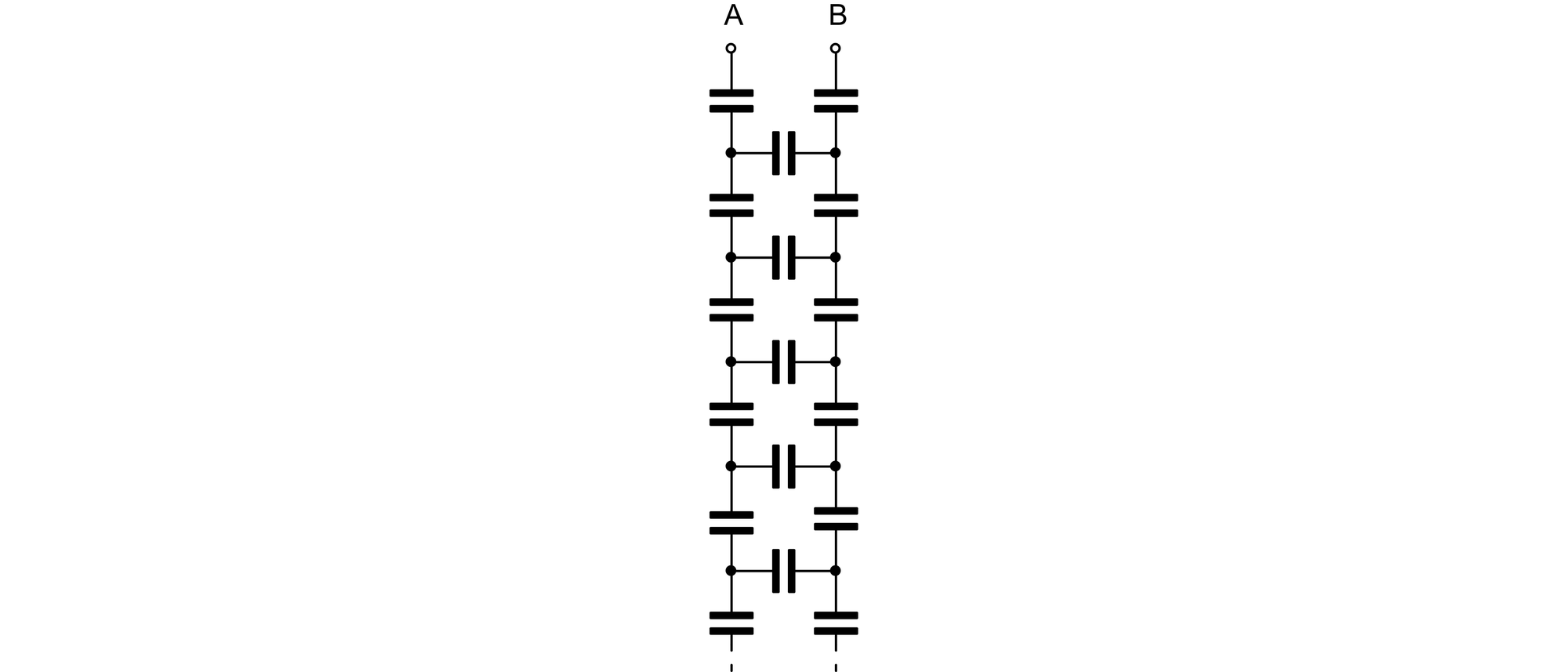
Aus unendlich vielen Kondensatoren ist eine unendlich lange Kondensatorleiter zusammengelötet worden. Alle Sprossenkondensatoren haben eine Kapazität von 2 µF und alle Holmkondensatoren von 3 µF. Wie groß ist die Gesamtkapazität zwischen den beiden oberen Enden A und B der Leiter?
Man kann die Kondensatorleiter im Gedanken in vier Bestandteile zerlegen: in die zwei obersten Holmkondensatoren C1, den obersten Sprossenkondensator C2 und den Rest der Leiter, der in der Skizze gelb unterlegt ist.
Da die Kondensatorleiter eine unendliche Länge hat, ist auch ihr Rest unendlich lang und darum identisch mit der Gesamtleiter. Bezeichnet man die Gesamtkapazität der Leiter zwischen den Punkten A und B mit C, beträgt auch die Gesamtkapazität der Restleiter C.
Die Gesamtkapazität der Leiter berechnet sich folglich aus einer Parallelschaltung eines Sprossenkondensators C2 und des Restleiterkondensators C, die mit zwei Holmkondensatoren C1 in Reihe geschaltet ist. Somit gilt 1/C = 1/C1 + 1/(C2 + C) + 1/C1. Nach C aufgelöst wird daraus C = ½(±√(C22 + 2C1C2) – C2).
Das Minuszeichen vor der Wurzel ergibt eine negative Gesamtkapazität, was aber physikalisch unsinnig ist. Darum bleibt als einzige Lösung C = ½(√(C22 + 2C1C2) – C2) = 1 µF.







Schreiben Sie uns!
Beitrag schreiben