Hemmes mathematische Rätsel: Finden Sie die Möglichkeiten!
Henry Ernest Dudeney (1857–1930) war wohl der bedeutendste Rätselerfinder, der jemals lebte. Das heutige Rätsel erschien 1924 im »Strand Magazine«.
Ein vollständiger Dominosatz besteht aus 28 Steinen, auf deren Feldern alle möglichen Zweierkombinationen von null bis sechs Augen gedruckt sind. Die beiden Felder jedes Steins sind jeweils durch einen Strich voneinander getrennt. Stellt man die Dominosteine auf ihre kurzen Seiten, lassen sie sich als Brüche deuten. Entfernt man aus dem Dominosatz die Steine, die eine Null oder zwei gleiche Augenzahlen enthalten, bleiben 15 übrig, die man so aufstellen kann, dass sie nur echte Brüche ergeben.
Wie viele verschiedene Möglichkeiten gibt es, die 15 echten Dominobrüche in drei Fünfergruppen aufzuteilen, damit die Summe jeder Gruppe den gleichen Wert hat?
Die Summe aller fünfzehn echten Dominobrüche beträgt 1/2 + 1/3 + 2/3 + 1/4 + 2/4 + 3/4 + 1/5 + 2/5 + 3/5 + 4/5 + 1/6 + 2/6 + 3/6 + 4/6 + 5/6 = 15/2. Folglich muss die Summe der fünf Brüche jeder Gruppe 5/2 ergeben. Zwölf dieser Brüche lassen sich zu Paaren kombinieren, die alle den Wert 1 haben, die restlichen drei haben jeweils den Wert 1/2.
1/3 + 2/3 = 1 1/4 + 3/4 = 1 1/2
1/5 + 4/5 = 1 2/5 + 3/5 = 1 2/4 = 1/2
1/6 + 5/6 = 1 2/6 + 4/6 = 1 3/6 = 1/2
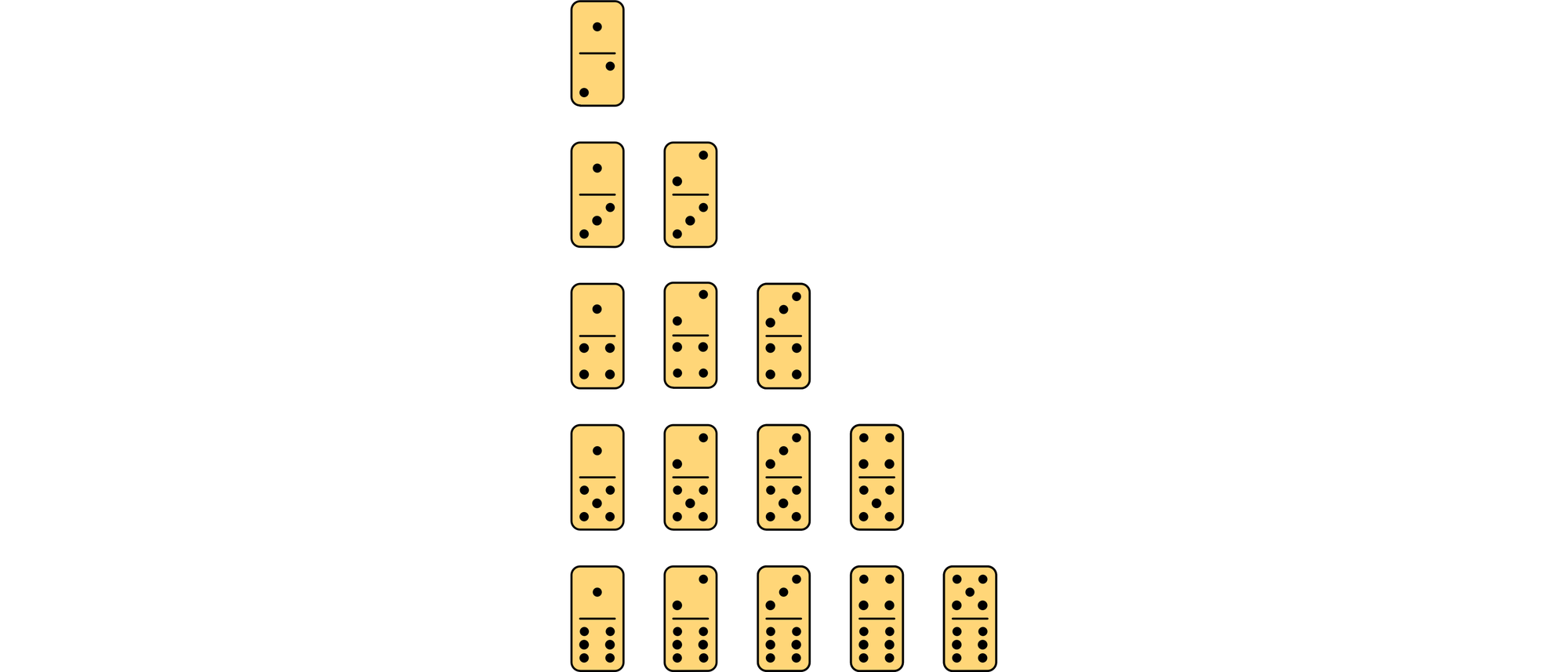
Aus diesen Paaren und Einzelbrüchen lassen sich leicht Fünfergruppen bilden, die jeweils die Summe 5/2 haben. Die Abbildung zeigt ein Beispiel.
Durch eine systematische Untersuchung lassen sich 186 verschiedene Möglichkeiten finden, wie man die fünfzehn echten Dominobrüche in drei Fünfergruppen aufteilen muss, damit die Summe in jeder Gruppe 5/2 beträgt.
Schreiben Sie uns!
Beitrag schreiben