Das heutige Rätsel stammt von der Betriebswirtin und Programmiererin Simone Falk-Hiller, die als Lehrbeauftragte an der Lüneburger Universität Leuphana arbeitet.

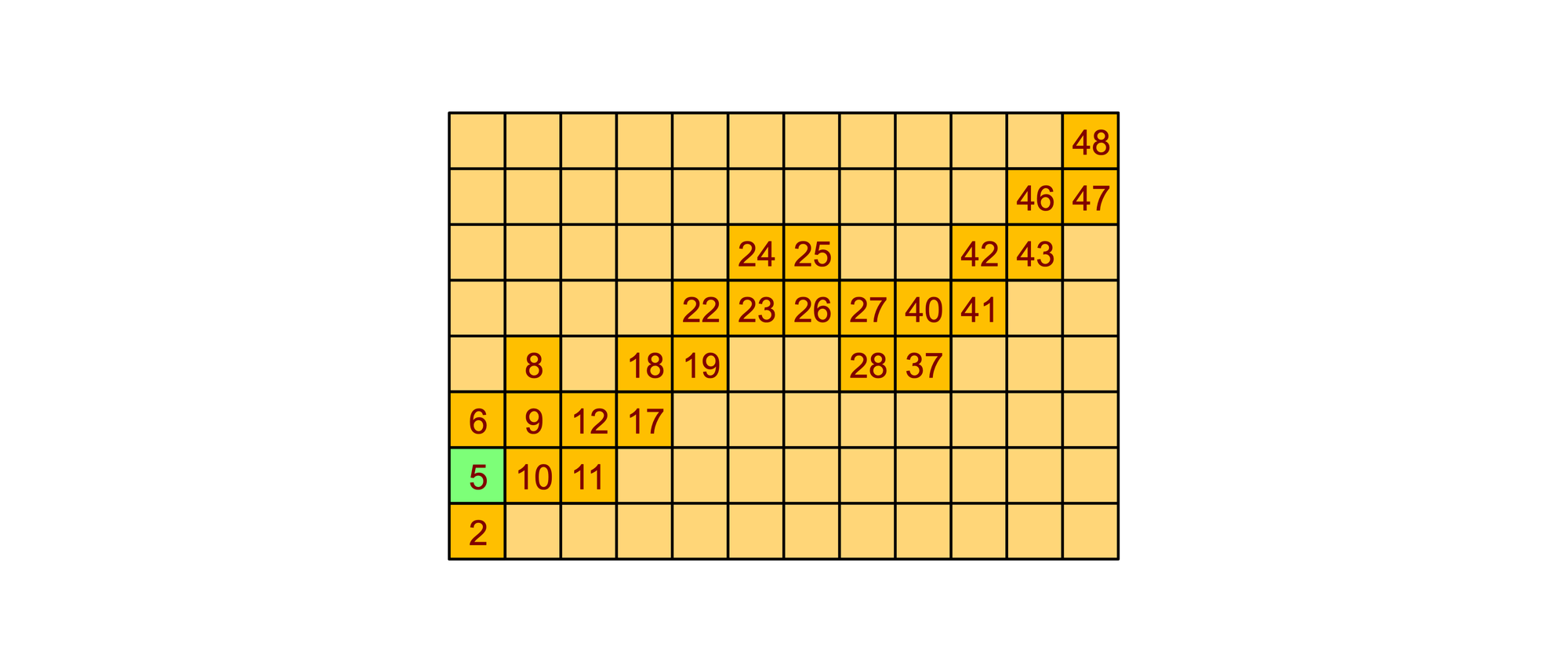
Über ein unendlich großes quadratisches Raster, von dem das Bild nur einen kleinen Ausschnitt zeigt, windet sich eine Zahlenschlange. Sie entsteht dadurch, dass man nacheinander alle natürlichen Zahlen 1, 2, 3, 4, … in das Raster schreibt.

Dabei wird zuerst die 1 in das grüne Feld gesetzt. Die Felder aller weiteren Zahlen werden dann nach einer bestimmten Regel gefunden. Steht in einem Feld bereits eine Zahl, überschreibt die größere Zahl die kleinere. Wie lautet die Regel?

Übrigens liegt keine der Zahlen von 1 bis 48 außerhalb des gezeigten Ausschnitts. Und alle Zahlen, die größer sind als 48, besetzen Felder, die außerdem des Ausschnitts liegen.