Hemmes mathematische Rätsel: In welchem Verhältnis steht der Inkreis zu dem kleinen Kreis?
© Heinrich Hemme (Ausschnitt)
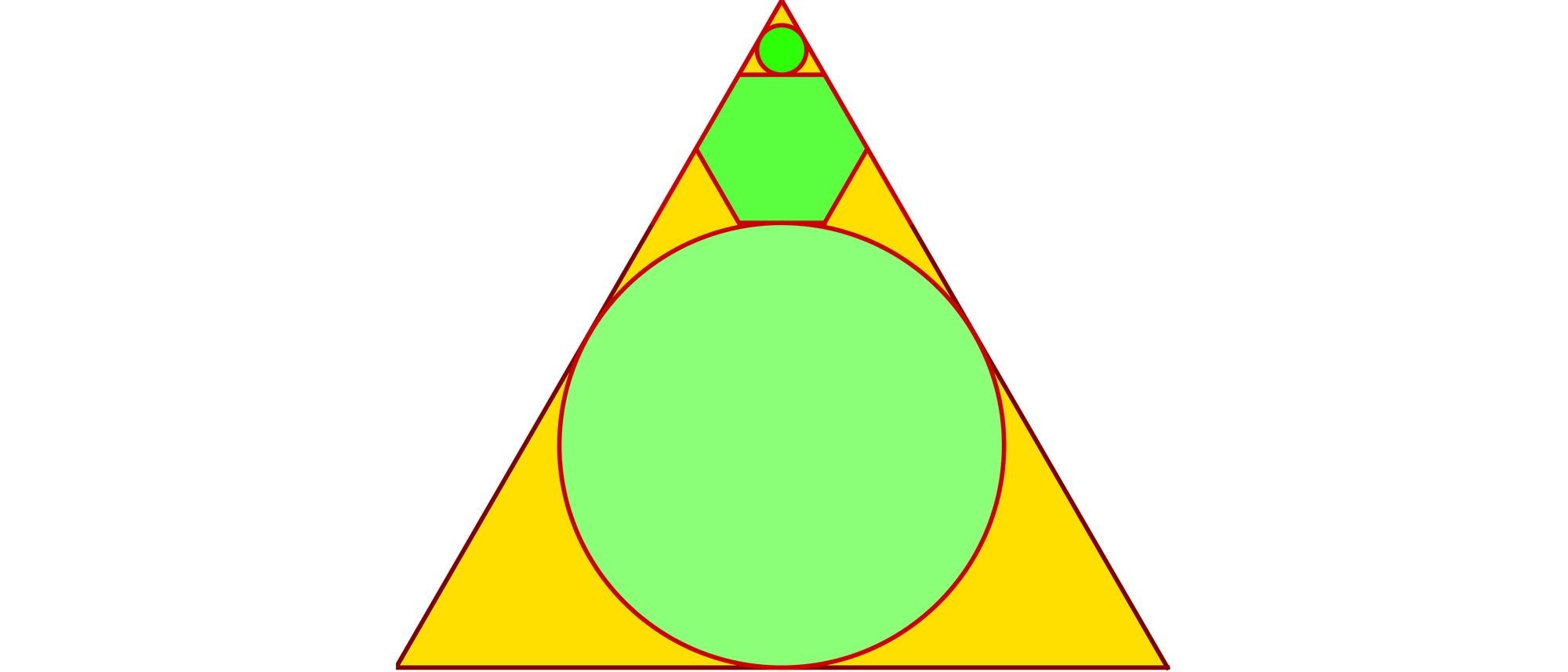
In einem gleichseitigen Dreieck liegen übereinander ein Inkreis, ein regelmäßiges Sechseck und ein kleiner Kreis. Die Figuren berühren sich, aber schneiden sich nicht. In welchem Verhältnis steht die Fläche des Inkreises zur Fläche des kleinen Kreises?
Überzieht man das Dreieck mit einem Raster aus kleinen Dreiecken, deren Seiten nur 1/9 der Länge der Seiten des großen Dreiecks haben, ist der kleine Kreis Inkreis eines kleinen Dreiecks und der große Kreis Inkreis des großen Dreiecks. Das Sechseck besteht aus sechs kleinen Dreiecken. Darum ist auch der Radius des großen Kreises das Neunfache des Radius des kleinen Kreises und der Flächeninhalt des großen Kreises das 92-Fache oder 81-Fache des Inhalts des kleinen Kreises.
© Heinrich Hemme (Ausschnitt)
Schreiben Sie uns!
Beitrag schreiben