Hemmes mathematische Rätsel: Stimmt die Behauptung?

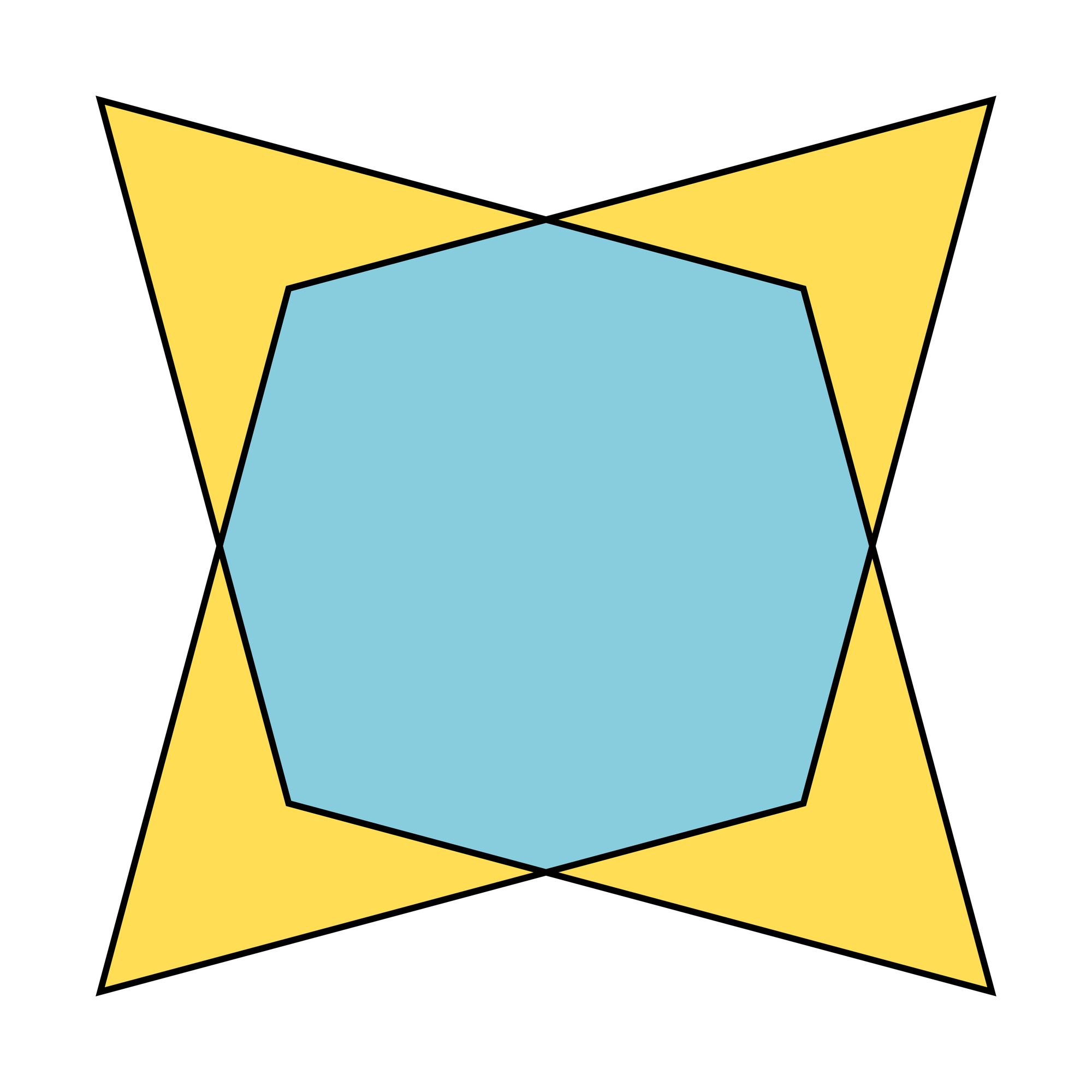
Die Fassade eines Hauses in Napier, einer Hafenstadt auf der Südinsel von Neuseeland, schmückt ein Jugendstilornament mit einem vierzackigen Stern. Es ist durch zwei gleiche, um 90 Grad gegeneinander verdrehte Rauten entstanden, die einen gemeinsamen Mittelpunkt haben. Jede Raute setzt sich aus zwei gleichseitigen Dreiecken zusammen. Jemand behauptet, die blaue Fläche sei mindestens anderthalbmal so groß wie die gelbe. »Stimmt das? Wie groß ist das exakte Verhältnis der beiden Flächenanteile?«, wollte Anfang 2023 Manfred Pietsch aus Kreuzau in Nordrhein-Westfalen von den Lesern und Leserinnen der Aachener Zeitung wissen.
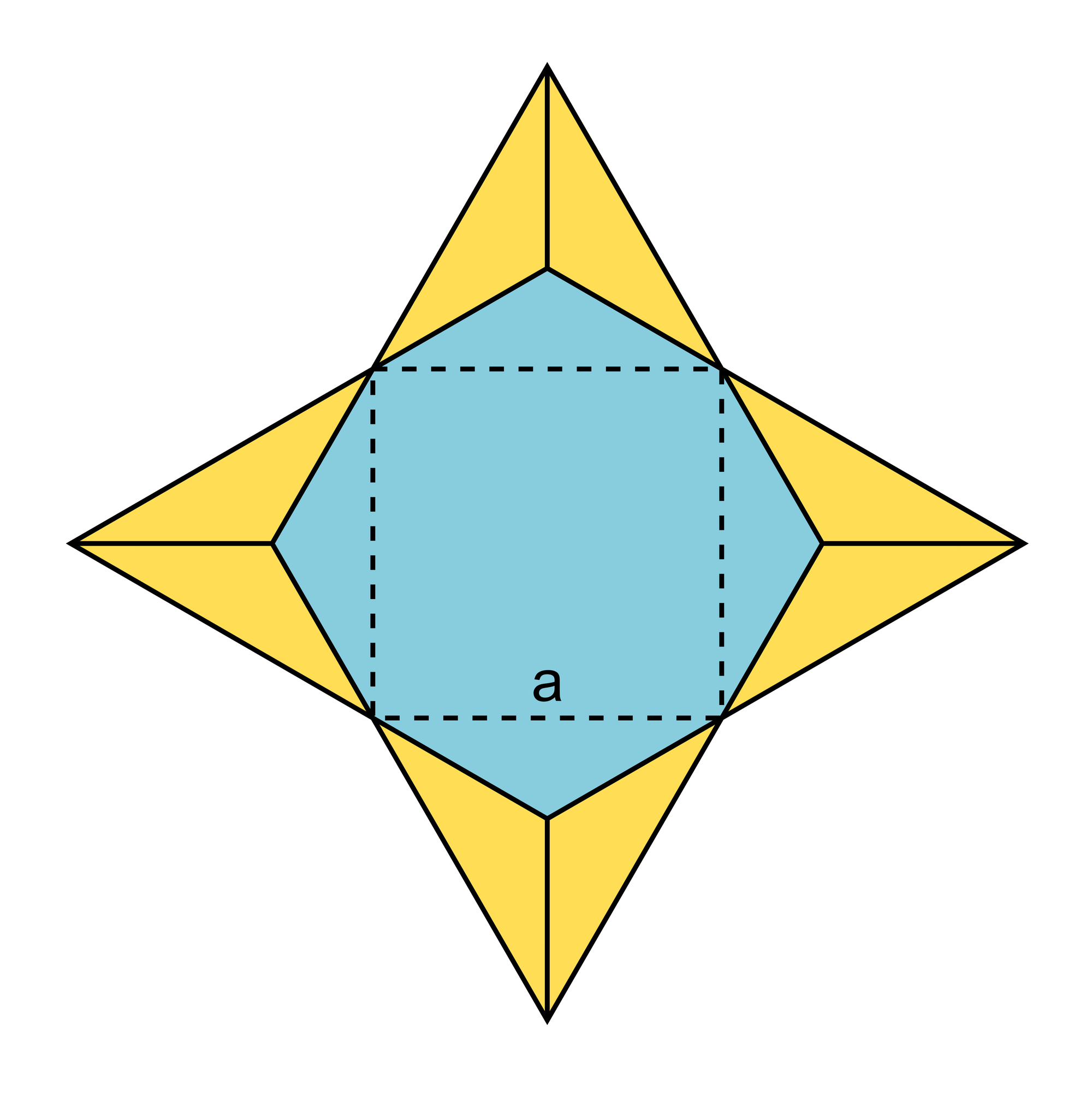
Wegen der Symmetrie des Sterns liegen seine vier konkaven Ecken auf den Ecken des gestrichelten Quadrates der Seitenlänge a und des Flächeninhalts a2. Die vier Zacken des Sterns sind gleichseitige Dreiecke, die auf den Quadratseiten stehen und zu zwei Dritteln gelb und zu einem Drittel blau sind. Jede Zacke hat die Fläche (√3)a2/4, und damit jedes Zackendrittel die Fläche (√3)a2/12. Die blaue Fläche besteht aus dem Quadrat und vier Zackendritteln und hat somit den Inhalt B = a2 + 4(√3)a2/12 = (1 + 1/3√3)a2. Die gelbe Fläche setzt sich aus acht Zackendritteln zusammen und hat darum den Inhalt G = 8(√3)a2/12 = 2/3(√3)a2. Das Verhältnis der blauen zur gelben Fläche beträgt folglich
B : G = (1 + 1/3√3)a2 : (2/3 (√3)a2), was man zu 1/2(1 + √3) ≈ 1,366 vereinfachen kann. Die blaue Fläche ist also nur um etwa 37 Prozent größer als die gelbe.









Schreiben Sie uns!
Beitrag schreiben