Hemmes mathematische Rätsel: Welche Werte kann n haben?
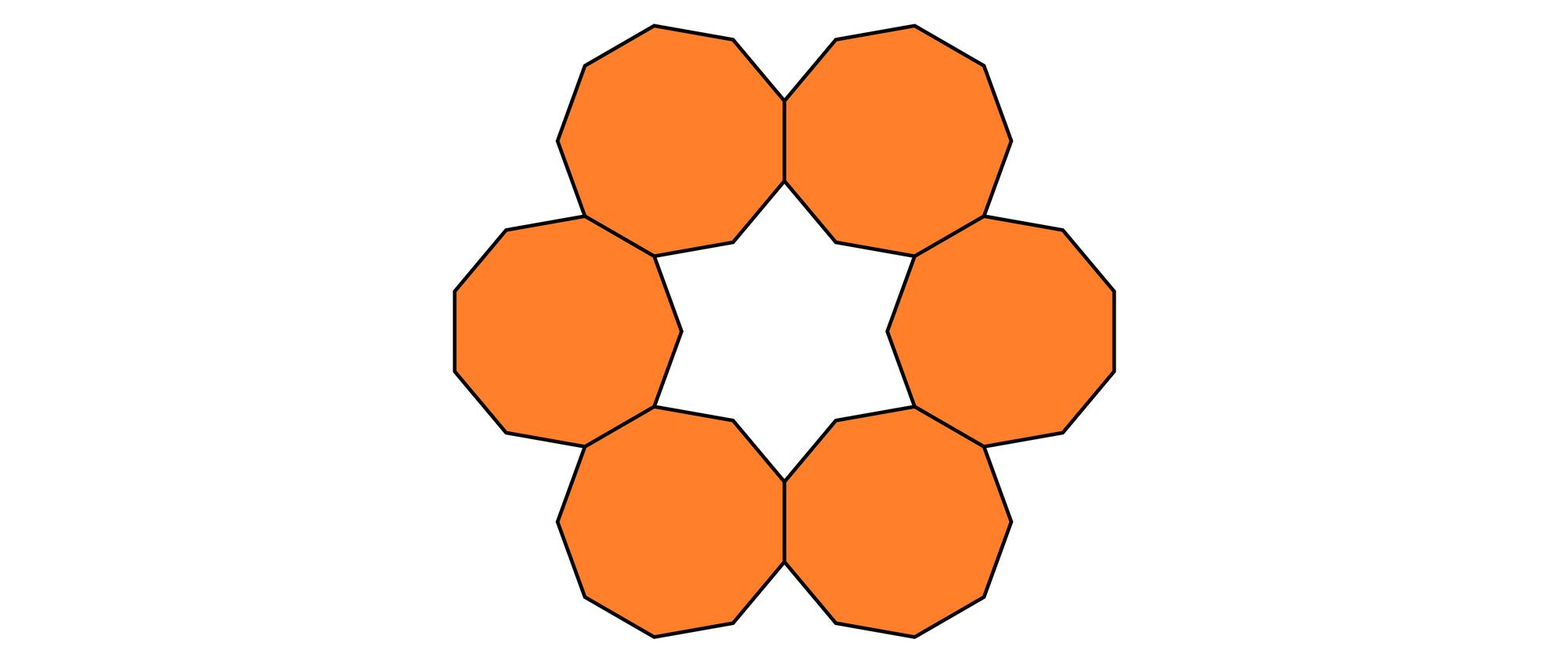
Ein Ring aus m gleich großen n-eckigen regelmäßigen Vielecken umschließt einen m-zackigen gleichseitigen Stern. Das Bild zeigt als Beispiel einen Stern für m = 6 und n = 9. Welche Werte kann n haben? Die Sternfläche muss größer als 0 sein.
Die Zentriwinkel und damit auch die Außenwinkel des regelmäßigen n-Ecks betragen α = 360°/n, und die Innenwinkel haben eine Größe von 180° – α = 180° – 360°/n. Verlängert man die Seiten der n-Ecke, die diese mit ihren Nachbarn gemeinsam haben, treffen sie sich im Mittelpunkt A des Sterns.
Da der Stern von m Polygonen gebildet wird, schließen die benachbarten Verlängerungen jeweils einen Winkel von 360°/m ein. Die Summe der Innenwinkel eines Vierecks beträgt stets 360°. Für das Viereck ABCD gilt darum 360°/m + 360°/n + (360° – (180° – 360°/n)) + 360°/n = 360°, was sich zu 2/m + 6/n = 1 oder 6m – mn + 2n = 0 zusammenfassen lässt. Die letzte Gleichung kann man auch als (m – 2)(n – 6) = 12 schreiben. Da ein Ring nicht aus weniger als drei Polygonen bestehen kann, ist m ≥ 3 und damit m – 2 positiv. Folglich muss auch n – 6 positiv sein, denn die rechte Seite der Gleichung ist positiv. Damit kann n – 6 nur 1, 2, 3, 4, 6 oder 12 sein und somit n nur 7, 8, 9, 10, 12 oder 18.
Schreiben Sie uns!
Beitrag schreiben