Hemmes mathematische Rätsel: Wie groß ist der Radius der Kreise?
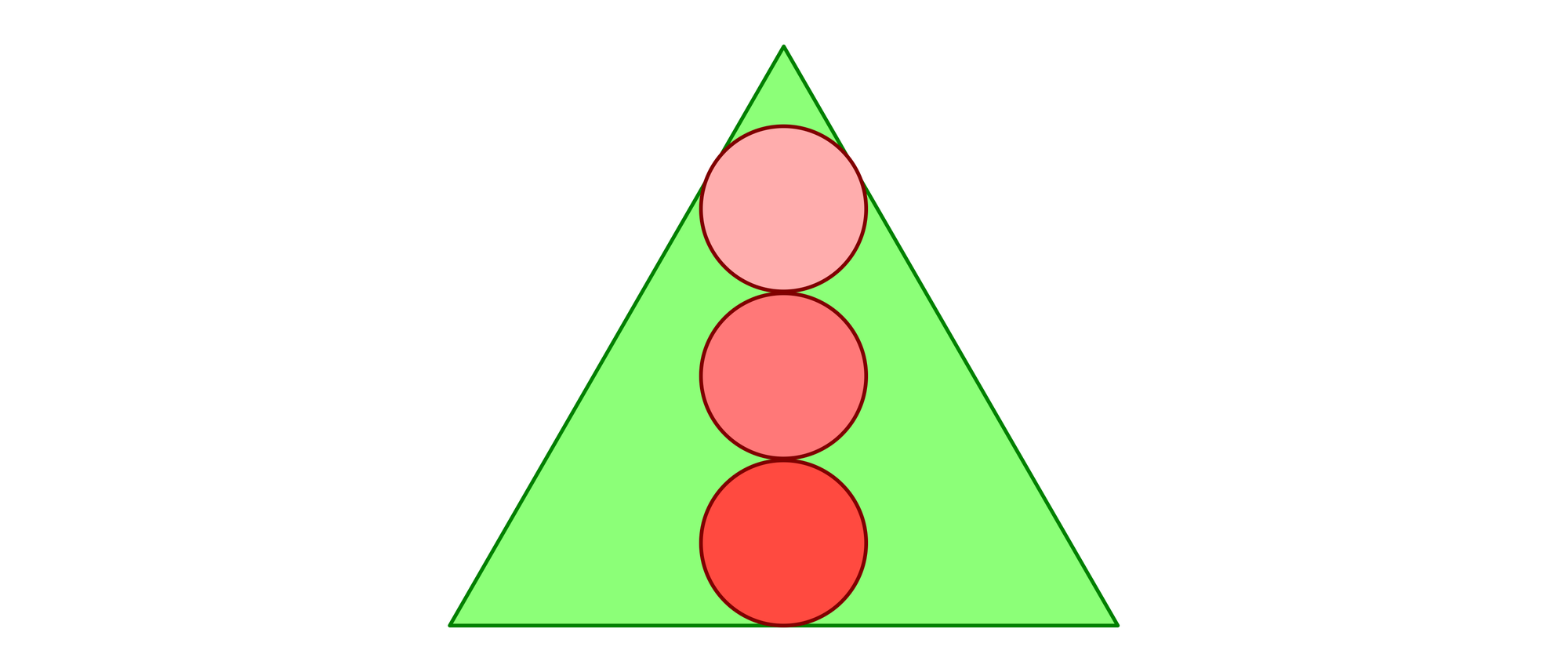
In einem gleichseitigen Dreieck der Seitenlänge 1 liegen drei gleich große Kreise übereinander. Wie groß ist der Radius dieser Kreise?
© Heinrich Hemme (Ausschnitt)
In einem gleichseitigen Dreieck der Seitenlänge 1 liegen drei gleich große Kreise übereinander. Wie groß ist der Radius dieser Kreise?
Der oberste der drei Kreise vom Radius r ist der Inkreis des gleichseitigen Dreiecks ADE. Die Winkelhalbierenden, deren Schnittpunkt I der Mittelpunkt dieses Kreises ist, zerlegen das Dreieck ADE in sechs gleiche rechtwinklige Dreiecke. Ihre spitzen Winkel sind 30° groß. Sie sind also halbierte gleichseitige Dreiecke. Deshalb sind ihre kurzen Katheten r und ihre Hypotenusen 2r lang. Damit hat die Höhe AJ des Dreiecks ABC die Länge 7r. Für das Dreieck ABJ gilt nach dem Satz des Pythagoras (1/2)2 + (7r)2 = 12, was sich zu r = √3/14 ≈ 0,1237 auflösen lässt.
© Heinrich Hemme
Schreiben Sie uns!
4 Beiträge anzeigen