Hemmes mathematische Rätsel: Wie groß ist der Winkel?
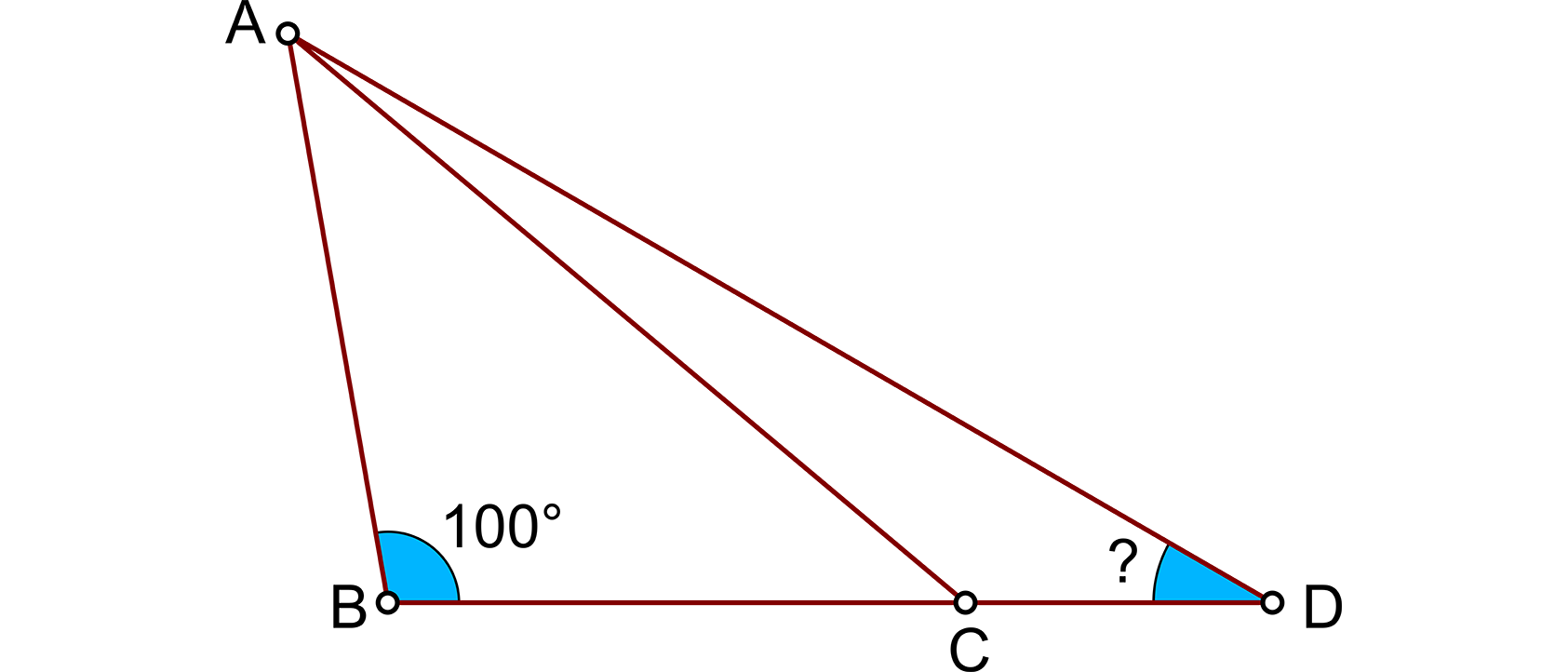
In der abgebildeten Figur sind die Strecken BA und BC gleich lang und schließen einen Winkel von 100° ein. BD und CA sind gleich lang. Die Strecken DB und DA schließen den mit einem Fragezeichen markierten Winkel ein. Wie groß ist er?
Das Dreieck ABC ist gleichschenklig, und da der Winkel ABC = 100° beträgt, sind die beiden Winkel BAC und ACB je 40° groß. Nun wird ein zum Dreieck ABC deckungsgleiches Dreieck DEB auf der Strecke BD errichtet. Die beiden Ecken A und E werden durch eine Strecke miteinander verbunden. Die Strecken AB, BE, AE und DE sind gleich lang. Folglich ist das Dreieck ABE gleichseitig, und die Winkel ABE, BAE und BEA sind 60° groß.
Das Dreieck DEB ist gleichschenklig, und seine Winkel BED, EDB und DBE sind 100°, 40° und 40° groß. Auch das Dreieck ADE ist gleichschenklig. Da der Winkel AED eine Größe von 100° + 60° = 160° hat, sind die beiden Winkel DAE und ADE je 10° groß. Daraus ergibt sich für den gesuchten Winkel CDA ein Wert von 40° – 10° = 30°.
Schreiben Sie uns!
4 Beiträge anzeigen