Hemmes mathematische Rätsel: Wie groß ist die Fläche?
© Heinrich Hemme (Ausschnitt)
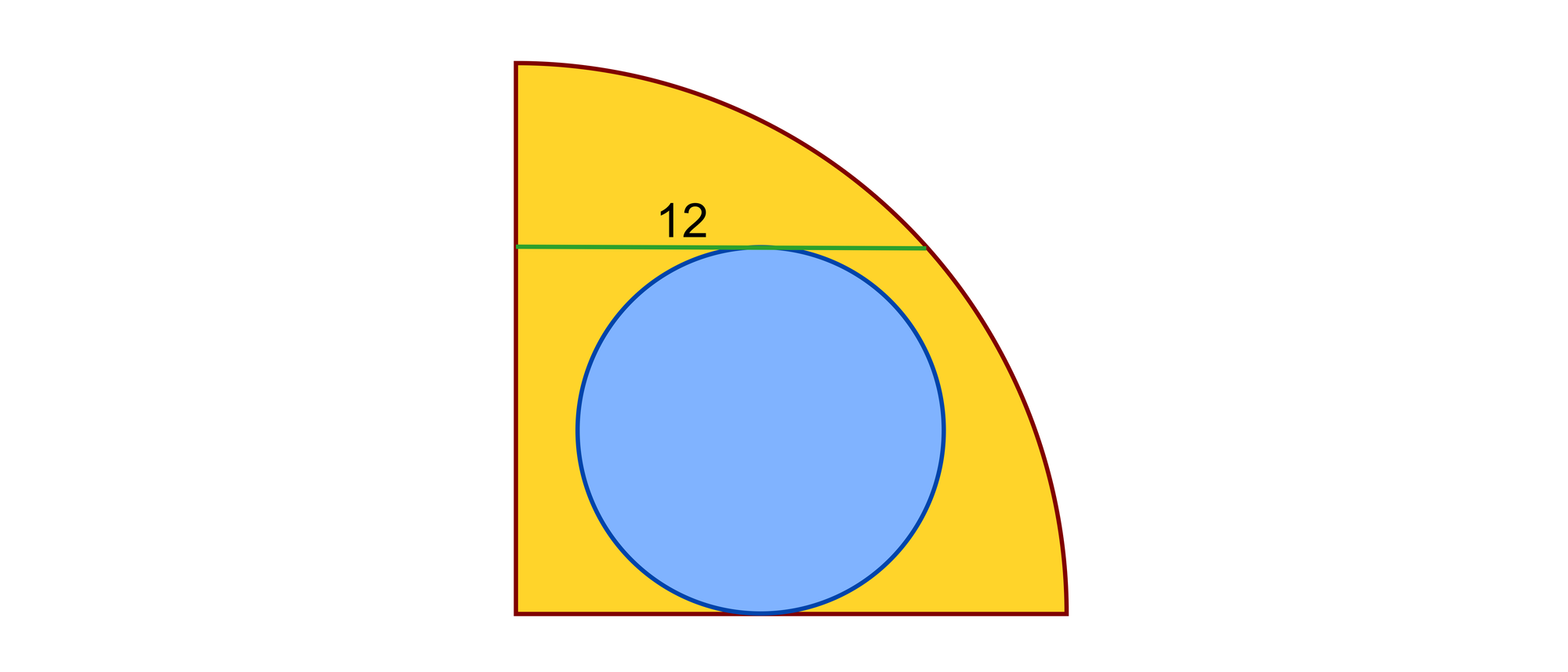
Durch einen Viertelkreis verläuft parallel zum unteren Radius eine Strecke der Länge 12, die den linken Radius mit dem Kreisbogen verbindet. Der blaue Kreis tangiert diese Strecke und den unteren Radius. Wie groß ist die gelbe Fläche?
Ist R der Radius des Viertelkreises und r der des Vollkreises, gilt für das rechtwinklige Dreieck ABC nach dem Satz des Pythagoras 122 + (2r)2 = R2. Dies kann man zu 1/4R2 – r2 = 36 umformen. Die gelbe Fläche ist die Differenz der Viertel- und der Vollkreisfläche und somit 1/4πR2 – πr2 = (1/4R2 – r2)π = 36π ≈ 113,1 groß.
© Heinrich Hemme (Ausschnitt)
Schreiben Sie uns!
Beitrag schreiben