Hemmes mathematische Rätsel: Wie lang ist das Rechteck?
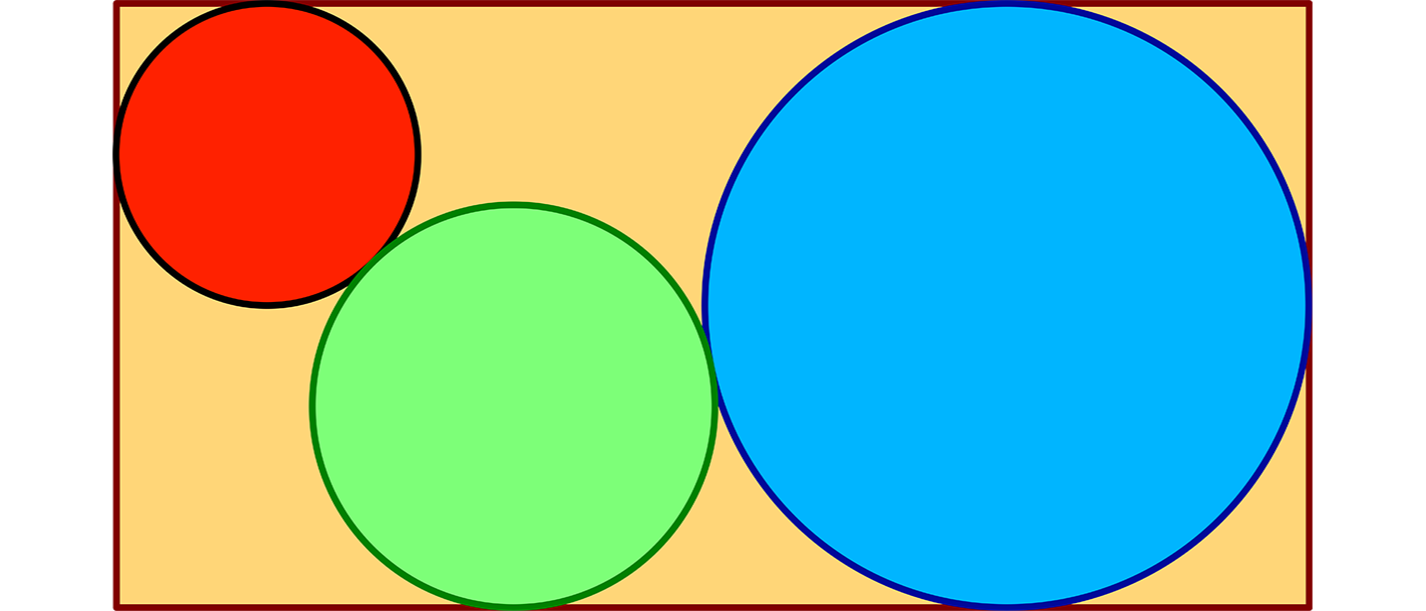
In einem Rechteck liegen, so wie es das Bild zeigt, drei Kreise. Der linke Kreis hat den Durchmesser 6, der mittlere 8 und der rechte 12. Wie lang ist das Rechteck?
A, B und C sind die Mittelpunkte der drei Kreise, und die Strecken AD und BE liegen parallel zu den langen und die Strecken BD und CE parallel zu den kurzen Rechteckseiten. Der Durchmesser des rechten Kreises und die Breite des Rechtecks haben die Länge 12. Folglich gilt BD = 12 – 3 – 4 = 5 und CE = 12 – 6 – 4 = 2. Die Hypotenusen der beiden rechtwinkligen Dreiecke ABD und BEC setzen sich aus den Radien der Kreise zusammen: AB = 3 + 4 = 7 und BC = 4 + 6 = 10. Daraus kann man mit dem Satz des Pythagoras die Längen der beiden horizontal verlaufenden Katheten berechnen zu AD = √((AB)2 – (BD)2) = √(72 – 52) = 2√6 und BC = √((BC)2 – (CE)2) = √(102 – 22) = 4√6. Somit hat das Rechteck die Länge 3 + AD + BE + 6 = 3 + 2√6 + 4√6 + 6 = 9 + 6√6 ≈ 23,697.
Schreiben Sie uns!
2 Beiträge anzeigen