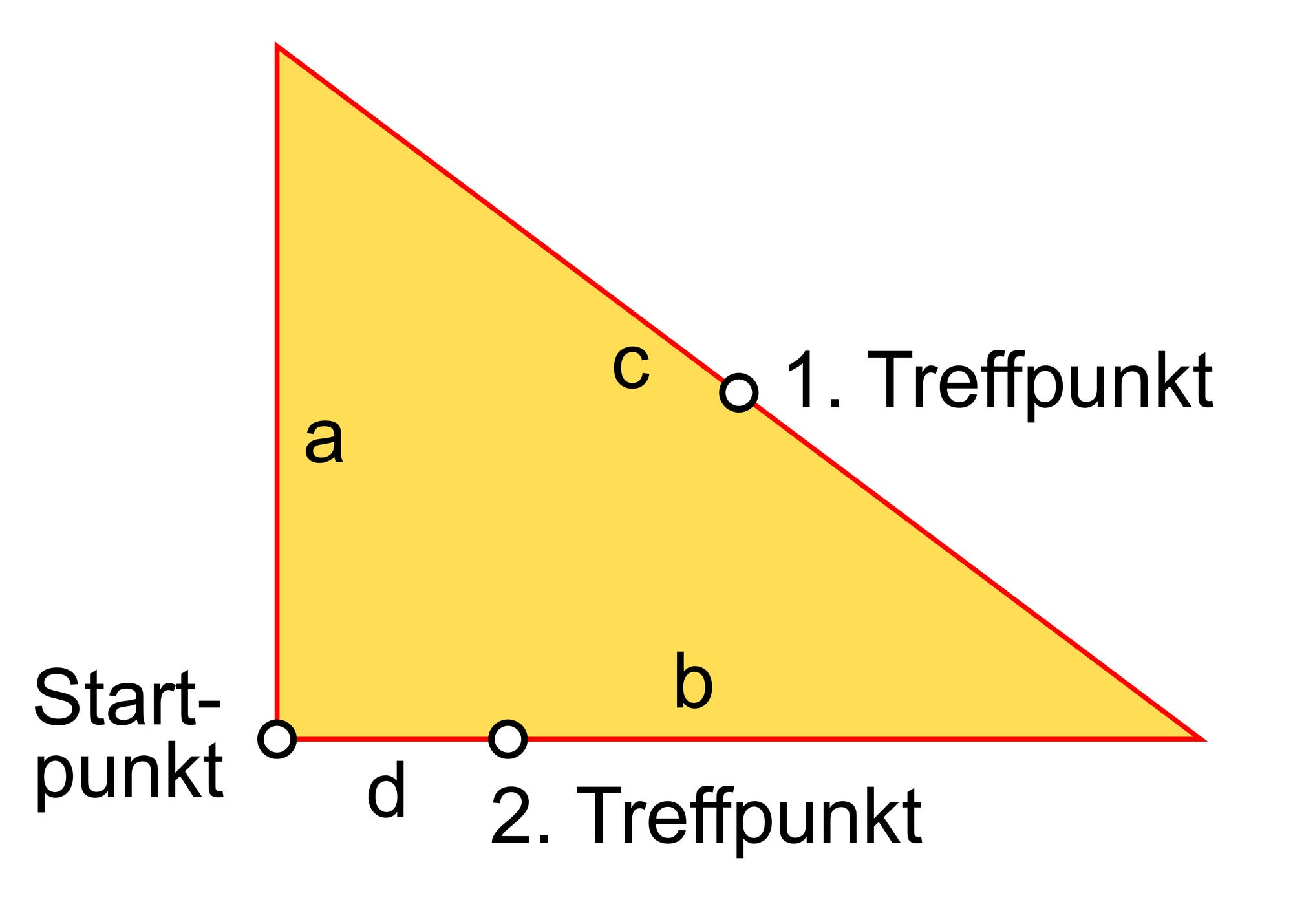
Das Feld mit den Seitenlängen a, b und c hat die Form eines rechtwinkligen Dreiecks, und es soll a < b < c sein. Nach dem Satz des Pythagoras gilt a² + b² = c². Beim ersten Treffen auf der Hypotenusenmitte hat der schnelle Junge den Weg b + c/2 zurückgelegt und der langsame den Weg a + c/2. Weil ihre Geschwindigkeiten im Verhältnis 13 : 11 stehen, gilt 13/11 = (b + c/2)/(a + c/2), was sich zu c = 11b – 13a vereinfachen lässt. Setzt man dies in die Pythagorasgleichung ein, erhält man a² + b² = (11b – 13a)². Dies kann man zu 84a² + 60b² = 143ab zusammenfassen. Beim zweiten Treffen hat der schnelle Junge das Feld ganz umrundet und noch d = 60 Meter von der zweiten Runde zurückgelegt. Dem langsamen Jungen hingegen fehlen noch d = 60 Meter von der ersten Runde. Somit gilt 13/11 = (a + b + c + d)/(a + b + c – d), was man zu a + b + c = 12d umformen kann. Fügt man in diese Gleichung c = 11b – 13a ein, erhält man a + b + 11b – 13a = 12d oder b = a + d. Dies wird nun in die Gleichung 84a² + 60b² = 143ab eingesetzt und ergibt 84a² + 60(a + d)² = 143ab. Nach einigen Umformungen bekommt man die quadratische Gleichung a² – 23da + 60d² = 0, die die Lösungen 3d und 20d hat. Die zweite Lösung ist sinnlos, da sie größer als der Umfang des Feldes ist. Somit ist a = 3d. Daraus ergeben sich auch sofort b = 4d und c = 5d. Die drei Seiten des Feldes sind somit 180 Meter, 240 Meter und 300 Meter lang.