Hemmes mathematische Rätsel: Um was für ein Dreieck handelt es sich?
2020 veröffentlichte Harald Burda aus Alsdorf bei Aachen in den »Aachener Nachrichten« und in der »Aachener Zeitung« ein geometrisches Problem:
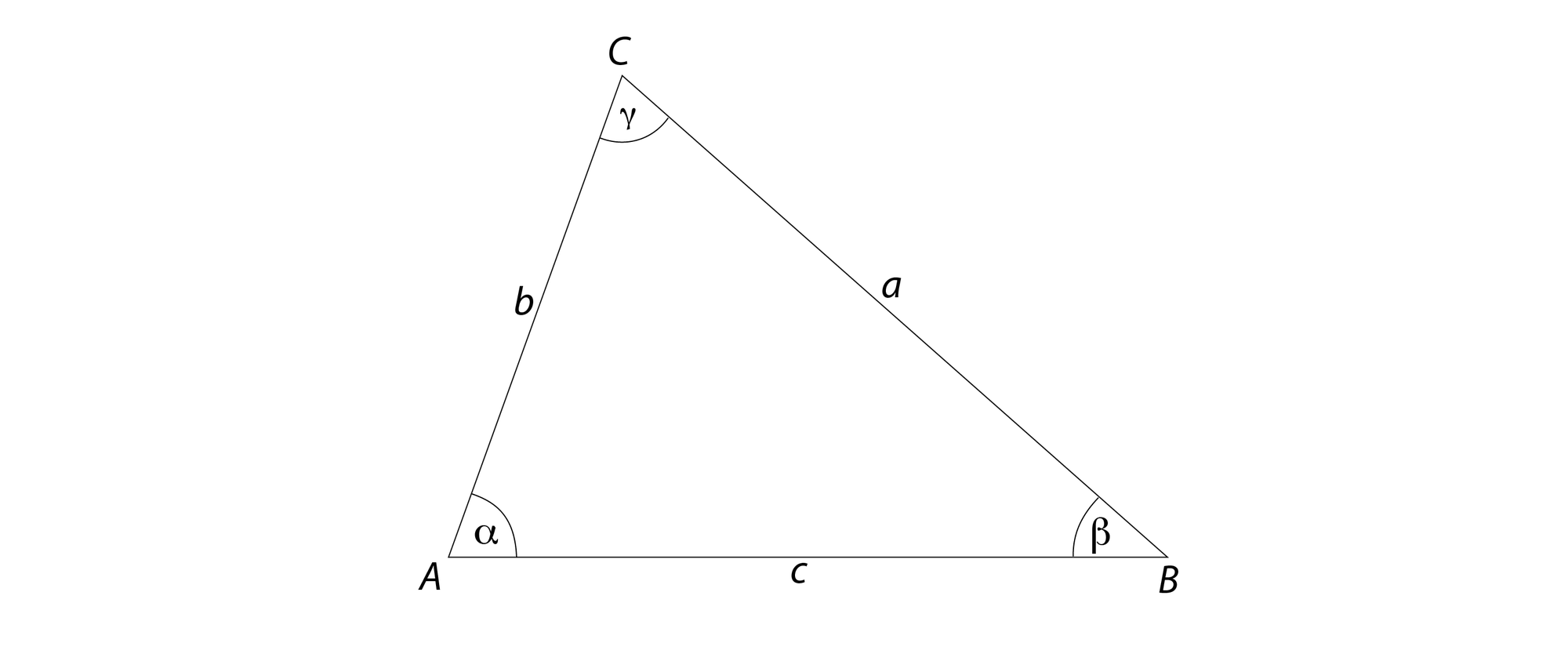
In einem Dreieck verhält sich die kurze zur mittleren Seite wie die mittlere zur langen Seite. Außerdem ist dieses Seitenverhältnis gleich dem Kosinus des Winkels, der von der mittleren und der langen Seite eingeschlossen wird. Ist dieses Dreieck gleichseitig, gleichschenklig, rechtwinklig, rechtwinklig gleichschenklig oder keines davon? In welchem Verhältnis steht die lange zur kurzen Seite?
Mit den Bezeichnungen aus der Skizze lassen sich die Bedingungen der Aufgabe als a < b < c und a/b = b/c = cos α schreiben. Aus der ersten Bedingung folgt, dass das Dreieck weder gleichseitig noch gleichschenklig sein kann. Da b/c zwischen 0 und 1 liegt, muss α zwischen 0° und 90° liegen. Für diesen Winkelbereich gilt cos α = x/c. Für spitz- und stumpfwinklige Dreieck ist x < b bzw. x > b, für rechtwinklige hingegen ist x = b. Und da cos α = b/c sein soll, ist das Dreieck rechtwinklig.
Die Gleichung a/b = b/c kann man zu b2 = ac auflösen. Setzt man dies in a2 + b2 = c2 ein, erhält man a2 + ac = c2, was man zu (c/a)2 − c/a − 1 = 0 umformen kann. Die quadratische Gleichung hat die positive Lösung c/a = (√5 + 1)/2 ≈ 1,618. Dieses Streckenverhältnis bezeichnet man als Goldenen Schnitt. Es wird seit der Antike in der Kunst und in der Architektur verwendet und als besonders ästhetisch empfunden.
Schreiben Sie uns!
Beitrag schreiben