Der Mathematische Monatskalender: Joseph Fourier (1768–1830)

Seinen Namen findet man, in goldenen Lettern geschrieben, unter den 72 Namen berühmter Franzosen auf einem Fries am Eiffel-Turm in Paris; sein Grab liegt an herausragender Stelle auf dem Friedhof Père Lachaise neben dem Grab von Gaspard Monge und von Jean-François Champollion. Aber während die französische Post diesen beiden bereits mehrere Briefmarken gewidmet hat, scheint man Joseph Fourier vergessen zu haben.
Jean-Baptiste Joseph Fourier wird als neuntes von zwölf Kindern aus der zweiten Ehe eines Schneiders in Auxerre (Burgund) geboren. Als er zehn Jahre alt ist, sterben seine Eltern kurz nacheinander; die Familie eines Verwandten nimmt ihn auf. Nach erfolgreichem Besuch einer Lateinschule an der Kathedrale von Auxerre wechselt er an die örtliche Militärschule, wo bald seine besondere Begabung für Mathematik und Physik erkennbar wird. Mit 19 Jahren tritt er dem Benediktiner-Orden bei – mit dem Gedanken, als Mathematiklehrer an der Klosterschule arbeiten zu können. Während der folgenden Monate zweifelt er an seinem Entschluss, hält weiter Kontakt zu seinem Mathematiklehrer in Auxerre, verfasst sogar einen Beitrag zur Algebra. Als er 21 Jahre alt wird, hadert er mit seinem Schicksal bei dem Gedanken, dass Newton und Pascal in diesem Alter bereits Unsterbliches vollbracht hatten. Er verlässt das Kloster, geht nach Paris, studiert Mathematik und kehrt als Lehrer für Mathematik an seine ehemalige Schule in Auxerre zurück.
Immer noch unentschlossen hinsichtlich seiner Zukunft, wird ihm durch die dramatische Veränderung der politischen Verhältnisse die Entscheidung abgenommen: 1793 tritt er dem örtlichen Revolutionskomitee bei. Dank seines Talents als Redner nimmt er bald Einfluss auf die Entwicklung der Revolution in der Region. Sein politisches Engagement kostet ihm fast den Kopf: Er legt sich mit der Robespierre-Fraktion an, und diese betreibt seine Inhaftierung. Der Guillotine entgeht er nur deshalb, weil seine Gegner nach der Hinrichtung von Robespierre selbst an Einfluss verlieren.
1794 wird Fourier für ein Mathematik-Studium an der neu eingerichteten École Normale in Paris ausgewählt; seine Lehrer sind Joseph-Louis Lagrange, Pierre-Simon Laplace und Gaspard Monge. Gleichzeitig wird der überragende Student als Lehrer am Collège de France tätig, wechselt zur neu gegründeten École Polytechnique. Erneut wird er wegen seiner Revolutionstätigkeit inhaftiert, aber bald wieder frei gelassen. 1797 übernimmt er die Nachfolge von Lagrange auf dessen Lehrstuhl für Analysis und Mechanik; sein Ruf als hervorragender Lehrer verbreitet sich.
1798 schließt er sich der Gruppe von Wissenschaftlern an, die Napoleon auf dessen Ägypten-Feldzug begleiten. Als die französische Flotte in der Schlacht im Nil-Delta durch die Flotte Admiral Nelsons vernichtet wird, ist die Expeditionsgruppe von der Heimat abgeschnitten.
Fourier kümmert sich um eine Reform des Schulwesens in Ägypten, wird zum Sekretär des Institut d' Égypte ernannt und organisiert archäologische Expeditionen. Napoleon beauftragt ihn auch damit, kostbare archäologische Fundstücke zu sammeln; selbst kehrt er nach Frankreich zurück, um dort die Herrschaft an sich zu reißen.
1801 kann auch Fourier nach Paris zurückkehren; am liebsten möchte er seine Tätigkeit als Mathematikprofessor fortsetzen. Napoleon jedoch ernennt ihn – gegen seinen Wunsch – zum Präfekten des Départements Isère. Zu seinen neuen Aufgaben gehört es, Sümpfe in der Region Lyon trockenzulegen und eine Straße von Grenoble nach Turin bauen zu lassen. Die Aufgaben erfüllt er zur großen Zufriedenheit seines Auftraggebers; er nimmt sich jedoch auch Zeit für zwei umfangreiche Schriften: Über die Ausbreitung von Wärme in festen Körpern und Description de l'Égypte.
Das Buch über Ägypten kann aber erst veröffentlicht werden, nachdem Napoleon sich in allen Darstellungen angemessen gewürdigt sieht – bei einem späteren Nachdruck des Werks nimmt Fourier fast alle Passagen, die Napoleons Verdienste betreffen, wieder heraus.
Seine Begeisterung für die alt-ägyptische Kultur ist ansteckend: Als er 1802 dem 12-jährigen Jean-François Champollion einen Abdruck des Steins aus Rosette zeigt, ist dieser von der Idee besessen, die auf dem Stein enthaltenen Zeichen zu entziffern. 1822 legt Champollion der Académie des Inscriptions et Belles-Lettres in Paris seine Forschungsarbeit vor: Die Hieroglyphen sind entschlüsselt!
Fouriers Werk über die Ausbreitung von Wärme in festen Körpern stößt nicht nur wegen der ungewohnten physikalischen Modellierung der Wärmeausbreitung auf Widerstand.
Auch die mathematische Behandlung des Problems wird von Lagrange und Laplace zunächst abgelehnt, da sie sich mit der Idee nicht anfreunden können, Funktionen mithilfe von Reihenentwicklungen trigonometrischer Funktionen darzustellen. Gleichwohl erhält Fourier für seine Arbeit im Jahr 1811 einen Preis der Académie des Sciences; das Komitee lehnt den Druck der Schrift jedoch ab.
1814 wird Napoleon abgesetzt und nach Elba verbannt; bei seiner Rückkehr marschiert er mit seinen neu gesammelten Truppen geradewegs auf Grenoble zu. Fourier versucht vergeblich, die Bürger Grenobles an ihren Treueeid zum König zu erinnern. Als Napoleon die Stadt betritt, flieht Fourier. Napoleon verzeiht ihm großmütig diesen »Verrat« an seiner Person und ernennt ihn zum Präfekten des Départements Rhône, verbunden mit einem hohen Gehalt, das jedoch nie ausgezahlt wird.
Nach der endgültigen Niederlage Napoleons kehrt Fourier nach Paris zurück, darf aber wegen seiner Kooperation mit Napoleon nicht wieder an seine alte Arbeitsstelle zurück. Auch verweigert der Bourbonen-König Louis XVIII ihm die Aufnahme in die Académie des Sciences, obwohl Fourier die meisten Stimmen unter den Kandidaten erhält. Erst 1817 wird er als Mitglied zugelassen. 1822 wählt die Académie ihn zum Ständigen Sekretär; vier Jahre später wird Fourier sogar in die Académie française aufgenommen, die Gesellschaft der 40 immortels (40 Unsterbliche).
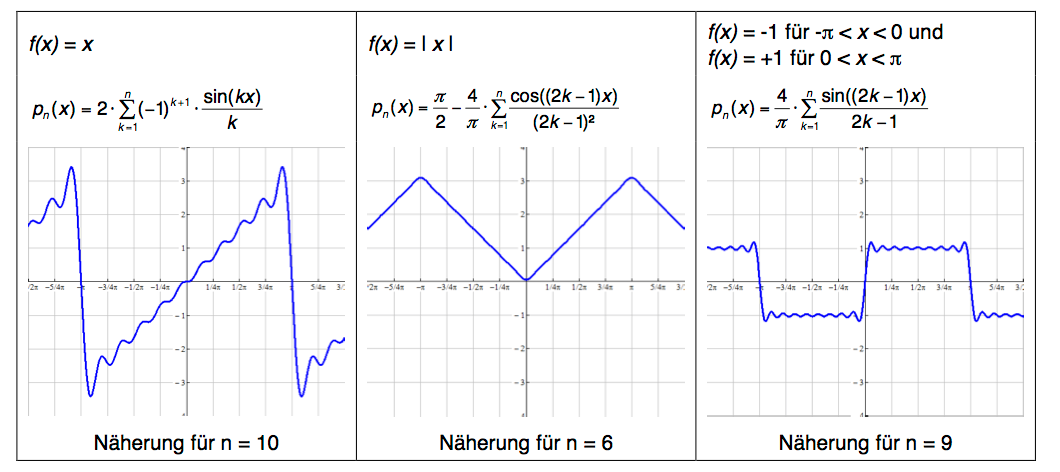
In seinen letzten acht Lebensjahren veröffentlicht er noch einige Abhandlungen zu mathematischen und physikalischen Problemen, darunter auch eine umfangreichere Fassung der Théorie analytique de la chaleur, in der er einen genialen Ansatz macht: Er behauptet: Jede periodische Funktion lässt sich als unendliche Summe von Sinus- und Kosinusfunktionen darstellen (heute so genannte Fourier-Reihe), konkret:
Ist \(f\) eine \(2\pi\)-periodische Funktion, dann existiert eine unendliche Reihe \(p_n\), die gegen \(f(x)\) konvergiert:
\(p_n(x)=\frac{1}{2}a_0+\sum_{n=1}^\infty \big(a_n\cos(nx)+b_n\sin(nx)\big).\)
Für die (Fourier)-Koeffizienten \(a_n\) und \(b_n\) gilt:
\(\begin{split} a_0&=\frac{1}{\pi}\int_0^{2\pi}f(x)\ dx,\\ a_n&=\frac{1}{\pi} \int_0^{2\pi}f(x)\cdot \cos(nx)\ dx,\\ b_n&=\frac{1}{\pi} \int_0^{2\pi} f(x)\cdot \sin(nx)\ dx. \end{split}\)
Ist \(f\) eine gerade Funktion, dann gilt \(b_n = 0\) für alle \(n\), ist \(f\) eine ungerade Funktion, dann entsprechend \(a_n = 0\) für alle \(n\), vergleiche Beispiele für das Intervall \( -\pi \leq x \leq +\pi\) :







Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.