Enzymkinetik, mathematische Behandlung enzymkatalysierter Reaktionen. Aus kinetischen Experimenten und durch Auswertung der erhaltenen Daten (kinetische Datenauswertung) erhält man eine Fülle an Informationen über Reaktionsmechanismen. Ein kinetisches Experiment besteht darin, unter kontrollierten Bedingungen für Temperatur, pH-Wert, Substrat- und Enzymkonzentration, Pufferzusammensetzung, usw. die Geschwindigkeit zu messen, mit der das Substrat verschwindet oder das Produkt erscheint. Die einfachste graphische Darstellung der Daten ist eine Zeit-Umsatz-Kurve, ein Diagramm, in dem Δ[S] gegen die Zeit aufgetragen wird (wobei [S] die Konzentration des Substrats ist). Das allgemeine Interesse gilt der Momentgeschwindigkeit v = d[S]/dt (Geschwindigkeitsgesetz), deren Bestimmung aus der Zeit-Umsatz-Kurve schwierig sein kann. Für diesen Fall kann ein integriertes Geschwindigkeitsgesetz oder der zeitliche Verlauf der Produktbildung nützlich sein. Die Aktivität eines Enzyms entspricht der Substrat- bzw. Produktmenge, die in einer gegebenen Zeit verbraucht bzw. gebildet wird. Das Nomenklatur-Kommitee der International Union of Biochemistry empfahl 1961 als Bezugsgröße die Verwendung der Enzymeinheit (U, Unit). 1U ist die Menge eines Enzyms, die benötigt wird, um 1Mikromol eines Substrats in einer Minute unter Standardbedingungen umzusetzen (Enzyme).
Einsubstrat-Enzyme zeigen eine Kinetik erster Ordnung. Die Geschwindigkeitsgleichung einer solchen unimolekularen oder pseudounimolekularen Reaktion lautet v = -d[S]/dt = k[S]. Die Reaktion wird durch die Halbwertszeit t_1/2 = ln2/k = 0,693/k charakterisiert, wobei k die Geschwindigkeitskonstante erster Ordnung ist. Die Relaxationszeit τ, d. h. die Zeit, die verstreicht, bis [S] auf 1/e des anfänglichen Werts gefallen ist, ist gegeben durch τ = 1/k = t_1/2/ln2.
Wenn an der Reaktion mehr als ein Substrat beteiligt ist (Multisubstrat-Enzyme), liegt eine Kinetik zweiter Ordnung (oder pseudozweiter Ordnung, Clelandsche Kurznotation) vor. Eine Reaktion zweiter Ordnung wird durch die Gleichung A + B

P wiedergegeben, mit k₂ als bimolekularer Geschwindigkeitskonstante und v = k₂[A][B]. Alle chemischen Reaktionen sind reversibel und erreichen eventuell einen Gleichgewichtszustand, in dem die Geschwindigkeiten der Hin- und Rückreaktionen gleich sind.
Die Gleichung einer reversiblen Reaktion ist gegeben durch A + B

P, wobei k₁ bzw. k₂ die Geschwindigkeitskonstanten der Hin- bzw. Rückreaktion sind. Die Gleichgewichtskonstante ist K = [P]/[A][B] = k₁/k₂.
Die Michaelis-Menten-Behandlung der Enzymkinetik setzt voraus, dass sich das Substrat und das Enzym vorübergehend zu einem Enzym-Substrat-Komplex verbinden, der entweder in das Substrat oder das Produkt zerfallen kann: E + S

ES

E + P. Für einen kurzen Zeitraum kann angenommen werden, dass die Geschwindigkeit, mit der sich [ES] ändert, klein ist verglichen mit der Änderung von [S] (Fließgleichgewichtsnäherung, steady state approximation), da die Geschwindigkeit der Bildung und des Zerfalls des ES-Komplexes gleich groß sind. Daraus ergibt sich, dass [E][S] =

[ES] = K_m[ES], wobei K_m die Michaelis-Konstante ist. Die Michaelis-Menten-Gleichung der Anfangsreaktionsgeschwindigkeit (wenn [P] = 0) lautet



Die Größen K_m und V_max werden als kinetische Parameter eines Enzyms bezeichnet (enzymkinetische Parameter). Eine graphische Darstellung der Anfangsreaktionsgeschwindigkeit in Abhängigkeit von der Substratkonzentration verläuft nichtlinear (Abb.). Deshalb ist es schwierig, aus dieser die kinetischen Parameter zu bestimmen (außer durch Computeranalyse).
Bei den bisherigen Betrachtungen wurde vorausgesetzt, dass die Rückreaktion vernachlässigt werden kann. Die Reaktionen, die von vielen Enzymen katalysiert werden, sind im wesentlichen irreversibel oder die Produkte sind sofort Gegenstand weiterer Reaktionen, so dass die Annahme der Irreversibilität Gültigkeit hat. Wenn die Reaktion jedoch reversibel ist, muss die Michaelis-Gleichung modifiziert werden. Haldane schlug eine Notation vor, in der V_H und V_R die Maximalgeschwindigkeiten der Hin- und Rückreaktionen sind und K_mS und K_mP die Michaelis-Konstanten von Substrat und Produkt. Damit ergibt sich für ein System mit einem einzigen Substrat und einem einzigen Produkt die Haldane-Beziehung K = V_fK_mP/V_rK_mS.
Multisubstrat-Enzyme katalysieren die Reaktionen von zwei oder mehr Substraten. Solche Enzyme können eine Reihe von verschiedenen Komplexen (Enzymspezies) mit einem oder beiden Substraten und/oder Produkten bilden. Die Reihenfolge, mit der diese Spezies gebildet werden, kann zufällig oder geordnet sein. Die Clelandsche Kurznotation bietet einen geeigneten Weg, diese Möglichkeiten darzustellen. Die Kinetik dieser Reaktionen wird extrem kompliziert. Die Gesamtheit der Reaktionen kann in Form von Enzymnetzwerken (Enzymgraphen) aufgezeigt werden. Zur Auswertung der kinetischen Daten eines solchen Systems wird ein Computer benötigt. Die Informationen, die mit Fließgleichgewichtsexperimenten gewonnen werden, reichen jedoch nicht aus. Es müssen schnelle Messmethoden eingesetzt werden, die es ermöglichen, Reaktionsmechanismen vor Einstellung des Fließgleichgewichts (pre-steady-state) untersuchen zu können, wie z. B. Stopped-Flow-, Temperatursprung- und Blitzlicht-Methoden (Relaxationsmethoden).

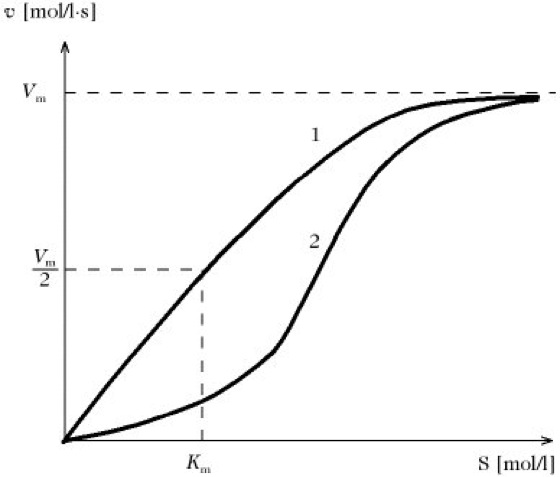
Enzymkinetik. Graphische Darstellung der Anfangsreaktionsgeschwindigkeit in Abhängigkeit von der Substratkonzentration, die gelegentlich auch Enzymkennlinie genannt wird. 1 = Michaelis-Menten-Hyperbel. 2 = sigmoide Kurve kooperativer Enzyme. Zu linearen Transformationen kinetische Datenauswertung.