Lexikon der Chemie: Destillation
Destillation, das wichtige Verfahren der thermischen Stofftrennung zur Isolierung und Reinigung von Flüssigkeiten durch Verdampfen und anschließende Kondensation des Dampfes. Durch Wärmezufuhr wird eine Flüssigkeit zum Sieden gebracht und der entstehende Dampf in einem Kühler als Destillat kondensiert. Da sich hier nur die Dampfphase bewegt, spricht man von Gleichstromdestillation. Wenn ein Teil des kondensierten Dampfes, der Rücklauf, dem aufsteigenden Dampf entgegengeführt wird und so in die Destillationsblase zurückläuft, spricht man von Gegenstromdestillation (Rektifikation).
Zur theoretischen Behandlung der D. ist die Kenntnis des Phasengleichgewichtes zwischen Dampf und zu trennender Flüssigkeit wichtig. Für die Partialdrücke pA und pB zweier Komponenten (A und B) im Dampfraum gilt nach dem Raoultschen Gesetz (ideales Verhalten vorausgesetzt):
pA = PA·xA und pB = PB·xB. (1)
Dabei sind PA und PB Dampfdrücke der reinen Komponenten A bzw. B, xA und xB Molenbrüche der Komponenten A bzw. B in der flüssigen Phase.
Da für eine binäre Mischung xB = 1 – xA ist, gilt für das Verhältnis der Partialdrücke im Dampfraum der Komponenten A und B:
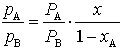
. (2)
Nach dem Daltonschen Gesetz sind die Partialdrücke pA und pB mit dem Gesamtdruck p über die Molenbrüche der beiden Komponenten im Dampfraum yA und yB gemäß
pA = p·yA bzw. pB = p·yB = p(1 – yA) (3)
verknüpft. Durch Einsetzen in (2) erhält man
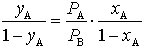
. (4)
Da x und y nach Übereinkommen ohne Angabe eines Indexes stets für die leichter flüchtige Komponente verwendet werden, nimmt (4) unter Einführung der relativen Flüchtigkeit α für ein ideales Zweistoffgemisch (α = pA/pB; Verhältnis der Dampfdrücke der reinen Komponenten) folgende Form an:
bzw.
. (5)
Nur wenn α größer ist als 1, ist eine Trennung durch D. möglich. Mit Hilfe von (5) läßt sich das y/x-Diagramm (Gleichgewichtsdiagramm, Abb. 1) berechnen. Ist die relative Flüchtigkeit α groß, so genügt zur Trennung eine einfache D. Diese wird im Labor in Destillationsapparaten aus Glas (Abb. 2), in der Technik in Destillationskolonnen aus Metall (Kolonne) durchgeführt.

Destillation. Abb. 1: Gleichgewichtsdiagramm eines idealen Zweistoffgemisches und Bestimmung der theoretischen Bodenzahl.

Destillation. Abb. 2: Labordestillationsapparat
Arbeitsweise. Das zu trennende Gemisch wird von einem beheizten Destillierkolben, in Destillationskolonnen von einer Blase aufgenommen. In einem Kühler (Kondensator) wird der mit der leichter flüchtigen Komponente angereicherte Dampf kondensiert, d. h. wieder verflüssigt und in einer Vorlage als Destillat aufgefangen. Soll eine höhere Anreicherung der leichten Bestandteile des Flüssigkeitsgemisches erzielt werden, so wird die D. in mehreren Stufen durchgeführt. Die fraktionierte D. wird angewandt, wenn mit einer einmaligen einfachen D. nicht die nötige Reinheit erreicht wird. Verdampft man ein binäres Gemisch mit der Sumpfkonzentration xS, so erhält man einen Dampf mit der Zusammensetzung y1. Kondensiert man diesen Dampf, so erhält man eine Flüssigkeit mit der Zusammensetzung x2. Mit dieser steht wiederum ein Dampf y2 im Gleichgewicht, dessen Kondensat einer Zusammensetzung x3 entspricht, usw. Man schreitet auf einer Stufenkurve zwischen der Gleichgewichtskurve und der 45°-Linie voran, bis die gewünschte Destillatkonzentration xD erhalten wird. Aus der Zahl dieser Stufen ergibt sich die für ein Trennproblem notwendige theoretische Bodenzahl. Es ist leicht zu erkennen, daß diese Zahl um so kleiner wird, je weiter die Gleichgewichtskurve von der 45°-Linie entfernt ist, d. h. je größer α ist. Die Trennwirkung einer Stufe hängt davon ab, bis zu welchem Grad sich der Austauschprozeß dem genannten Gleichgewicht nähert. Die Wirksamkeit einer Destillationskolonne wird gekennzeichnet durch die Angabe der Trennstufenzahl (Bodenzahl). Der stufenweise Trennprozeß kann in einer einzigen Kolonne verwirklicht werden. Die praktische Trennstufenzahl wird dabei durch besondere Konstruktionselemente (Böden) erhöht, die eine rasche Durchmischung und eine große Berührungsfläche der Phasen ermöglichen. Die bisher gemachten Aussagen gelten nur für den Fall, daß bei der Rektifikation kein Destillat abgenommen wird und das gesamte Kondensat wieder durch die Trennsäule zurückfließt (totaler Rücklauf). Da unter praktischen Verhältnissen dieses Gleichgewicht ständig gestört wird, indem ein Teil des Kondensates als Destillat aus dem Prozeß herausgenommen wird und nur der verbleibende Teil des Kondensates als Rücklauf in die Kolonne zurückfließt, ergibt sich folgende Stoffbilanz:
Gesamtmenge verdampfter Flüssigkeit (G) = Rücklauf (R) + Destillat (D). (6)
Multipliziert man mit den entsprechenden Konzentrationsfaktoren y = Konzentration des Dampfes, x = Konzentration der Flüssigkeit und xD = Konzentration des Destillats, so erhält man durch Einsetzen in (6) und Umformung
. (7)
Durch weitere Umformung und Einführung des Rücklaufverhältnisses ν = R/D wird eine Geradengleichung (8) erhalten mit der Steigung ν/(1 + ν) und dem Ordinatenabschnitt xD(1 + ν):
. (8)
Diese Arbeitsgerade tritt unter praktischen Bedingungen an die Stelle der 45°-Linie zur Bestimmung der theoretischen Bodenzahl. Die Trennstufenkurve muß jetzt zwischen Arbeitsgerade und Gleichgewichtskurve eingezeichnet werden (Abb. 3).
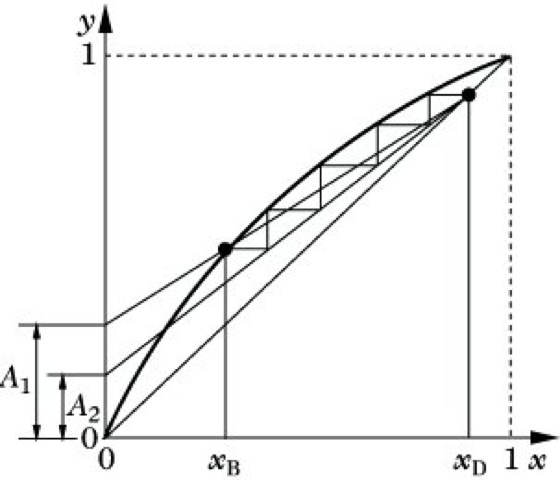
Destillation. Abb. 3: Bestimmung der theoretischen Bodenzahl nach dem Verfahren von Thiele-McCabe.
Abb. 3 sind folgende Grenzfälle zu entnehmen:
1) Die Arbeitsgerade mit dem Ordinatenabschnitt A1 geht durch den Punkt der Gleichgewichtskurve mit dem Abszissenwert xB. Für diesen Fall können unendlich viele Stufen zwischen Arbeitsgerade und Gleichgewichtskurve eingezeichnet werden. Bei diesem Rücklaufverhältnis sind also unendlich viele Böden für die Trennung notwendig. Es wird darum als minimales Rücklaufverhältnis bezeichnet und darf für das jeweilige Trennproblem nicht unterschritten werden.
2) Wird das gesamte Kondensat als Rücklauf in die Kolonne zurückgeführt (d. h. bei unendlichem Rücklaufverhältnis), geht die Arbeitsgerade in die 45°-Linie über. Die sich jetzt ergebende Stufenzahl wird minimale Bodenzahl genannt, d. i. die Stufenzahl, die für das konkrete Trennproblem nicht unterschritten werden darf.
Einen praktischen Fall zeigt die Arbeitsgerade mit dem Ordinatenabschnitt A2. Innerhalb der beiden Grenzen minimale Bodenzahl und minimales Rücklaufverhältnis kann man eine fehlende Bodenzahl durch ein größeres Rücklaufverhältnis kompensieren und umgekehrt.
Die D. kann entweder diskontinuierlich oder kontinuierlich durchgeführt werden. a) Bei der diskontinuierlichen D. wird ein dem Fassungsvermögen der Apparatur angepaßter Vorrat des zu trennenden Flüssigkeitsgemisches verdampft. Die einzelnen Bestandteile erscheinen entsprechend ihren Siedepunkten oder Siedebereichen in mehr oder weniger reinem Zustand nacheinander im Kondensat und können getrennt aufgefangen werden. b) Bei der kontinuierlichen D. wird das zu trennende Gemisch kontinuierlich der Kolonne zugeführt, und die getrennten Produkte werden über Kopf bzw. aus dem Sumpf abgezogen. Den Teil der Kolonne zwischen Einspritzung und Kondensator nennt man Verstärkersäule, den Teil zwischen Sumpf und Einspritzung Abtriebssäule (Abb. 4).
Ein Zweikomponentengemisch (A und B) kann mit Hilfe einer Kolonne in ein Kopfprodukt A und ein Sumpfprodukt B zerlegt werden. Für ein Dreikomponentengemisch A, B und C sind mindestens zwei Kolonnen notwendig, wenn alle drei Komponenten in reiner Form isoliert werden sollen. Ein Mehrkompontengemisch kann auch an einer Kolonne mit Seitenstromabnahme zerlegt werden.

Destillation. Abb. 4: Kontinuierliche Destillation eines Zweistoffgemisches. A Leichter flüchtige Komponente (Destillat), B Sumpfprodukt.
Zur Trennung hochsiedender und temperaturempfindlicher Flüssigkeitsgemische bedient man sich bei Drücken von 0,1 bis 2,5 kPa der Vakuumdestillation, bei Drücken von etwa 10-2 Pa der Hochvakuumdestillation.
Höchsten Ansprüchen genügt die Molekulardestillation. Der Abstand zwischen Flüssigkeitsoberfläche und stark gekühlter Kondensationsfläche muß dabei in der Größenordnung der mittleren freien Weglänge der Dampfmoleküle liegen. Dadurch trifft das verdampfte Molekül ohne vorherigen Zusammenstoß mit anderen Gasmolekülen auf die Kondensatoroberfläche. Auf diesem Wege ist z. B. die destillative Trennung der Quecksilberisotope gelungen.
Bei zahlreichen, mit Wasser nicht oder nur wenig mischbaren Flüssigkeiten gelingt wie bei der Vakuumdestillation die Herabsetzung der Siedetemperatur auch durch Einblasen von Wasserdampf in die Destillierblase (Wasserdampfdestillation, Trägerdampfdestillation). Anstelle von Wasser können auch andere, nicht mischbare Flüssigkeiten benutzt werden. Die Wasserdampfdestillation kann mit der Vakuumdestillation kombiniert werden.
Bei nicht idealen Flüssigkeitsgemischen besitzt die Gleichgewichtskurve einen ausgezeichneten Punkt, den azeotropen Punkt, in dem sie die 45°-Linie schneidet. Zur Trennung dieser und eng siedender Gemische wird die Azeotropdestillation, die Extraktivdestillation oder die D. bei verschiedenen Systemdrücken angewendet.
Bei der trockenen D. organischer Stoffe (unter Luftabschluß) werden gasförmige oder flüssige sowie feste Zersetzungsprodukte gebildet. So entstehen bei der trockenen D. der Steinkohle Rohgas, Teer und Koks; durch trockene D. von Holz werden z. B. Methanol, Essigsäure, Holzteer und Holzkohle gewonnen.
Die Anwendung der D. in der chem. Industrie und im Laboratorium ist äußerst vielseitig. So wendet man die D. beispielsweise an zur Zerlegung des gereinigten Rohöls in Leichtbenzin, Schwerbenzin, Gasöl und Asphalte, zur Abtrennung des Benzols vom Waschöl der Kokereien, zur Gewinnung von Stickstoff, Sauerstoff und Edelgasen aus verflüssigter Luft u. a.
Da die D. zu den energetisch sehr aufwendigen Trennprozessen gehört, hängt die Wirtschaftlichkeit einer destillativen Stofftrennung wesentlich vom Heizdampf- und vom Kühlwasserverbrauch ab. Möglichkeiten zur Energieeinsparung bieten die Kaskadenverdampfung und die Brüdenverdichtung.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.