Potentialhyperfläche, Fläche, die die Abhängigkeit der potentiellen Energie mehrerer Atome (z. B. in einem Molekül) von den geometrischen Anordnungen ihrer Kerne darstellt. Voraussetzung für die Definition der P. ist die Entkopplung von Kern- und Elektronenbewegung (Born-Oppenheimer-Näherung).

Die potentielle Energie ε_pot für die Bewegung der Atomkerne im Molekülverband ist prinzipiell quantenchemisch berechenbar, indem man jeweils für eine vorgegebene Kernanordnung die Schrödinger-Gleichung des Gesamtsystems löst. Der niedrigste erhaltene Energiewert entspricht einem Punkt auf der P. des Grundzustandes, die höheren Eigenwerte sind Punkte auf darüber liegenden P. angeregter Zustände. Durch systematische Variation der Kernkoordinaten wird die P. punktweise berechnet.

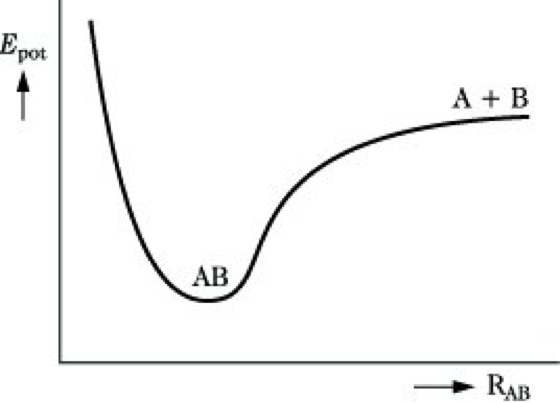
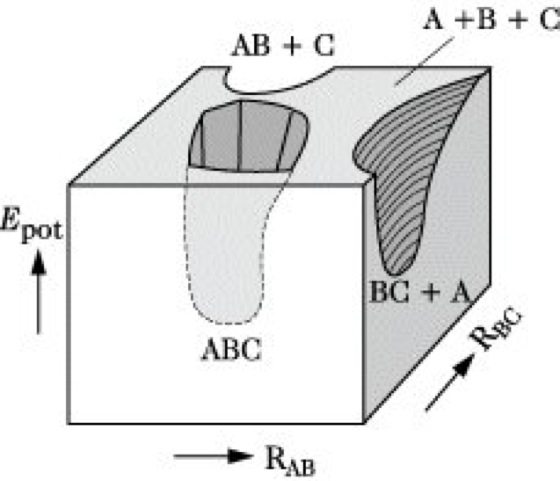
Die P. eines stabilen zweiatomigen Moleküls AB hängt nur vom Kernabstand R_AB ab, stellt also eine Potentialkurve der ε_pot-R_AB-Ebene dar (Abb. 1). Ein dreiatomiges Molekül ABC erfordert zur genauen Festlegung der Kernkonfiguration drei Koordinaten, z. B. die Bindungsabstände R_AB, R_BC und R_AC oder R_AB, R_BC und den Bindungswinkel zwischen diesen beiden Bindungen. Ist der letztere fest, z. B. 180° in einem linearen Molekül, so reichen die zwei Abstände R_AB und R_BC, weil für R_AC stets R_AC = R_AB + R_BC gilt. Die P. ist dann eine Fläche im ε_pot-R_AB-R_BC-Diagramm (Abb. 2). Analog läßt sich die P. einer Reaktion AB + C → A + BC darstellen, wenn man voraussetzt, daß sich C linear in Bindungsrichtung an AB annähert. Allerdings liegt auf der Seite der Ausgangsstoffe das ungestörte Molekül AB in einem Minimum potentieller Energie bei großem Abstand R_BC, auf der Produktseite befindet sich BC bei großem R_AB in einem Minimum. Beide Minima sind durch einen Bereich höherer potentieller Energie getrennt (Abb. 3).

Potentialhyperfläche. Abb. 1: Potentialkurve eines zweiatomigen Moleküls AB.

Potentialhyperfläche. Abb. 2: Schnitt durch die Potentialfläche eines linearen dreiatomigen Moleküls ABC.

Potentialhyperfläche. Abb. 3: Schnitt durch die Potentialfläche für die Reaktion A + BC → AB + C.

Die Kurve von AB zu BC auf dem Weg minimaler potentieller Energie wird Reaktionskoordinate genannt. In der Theorie des Übergangszustandes (Reaktionskinetik, Theorie) spielt der Sattelpunkt der P., d. h. der höchste Energiewert auf der Reaktionskoordinate, eine zentrale Rolle. Befinden sich die reagierenden Teilchen AB und C in diesem Sattelpunkt, so werden sie als aktivierter Komplex oder Übergangszustand bezeichnet. Die Differenz der potentiellen Energien zwischen Sattelpunkt und den Ausgangsstoffen ist die Schwellenenergie. Systeme aus N Atomen erfordern 3 N – 6 Kernkoordinaten zur Festlegung der Konfiguration, liefern also mehrdimensionale Flächen im 3 N - 5-dimensionalen Raum. Lokale Minima entsprechen stabilen oder metastabilen Verbindungen, Sattelpunkte den Übergangszuständen. Die ausschnittsweise Berechnung und Interpretation von P. ist eine zentrale Aufgabe der modernen Quantenchemie und eine wichtige Grundlage der theoretischen Reaktionskinetik.

Reaktionen, die auf einer P. ablaufen, bezeichnet man als adiabatisch.