Lexikon der Geowissenschaften: Röntgenstrukturanalyse
Röntgenstrukturanalyse, Bestimmung der räumlichen Anordnung der Atome einer Kristallstruktur durch Röntgenbeugungsmethoden. Für eine Kristallstruktur, deren Atome dreidimensional periodisch auf ineinandergestellten, kongruenten Translationsgittern angeordnet sind, beobachtet man mit Röntgenstrahlung Interferenzeffekte, ähnlich wie mit Licht an einem optischen Strichgitter. Konstruktive Interferenz tritt nur dann auf, wenn der Streuvektor:
zwischen der Richtung des einfallenden Strahls ![]()
0 und der Richtung des gebeugten Strahls ![]()
mit einem reziproken Gittervektor:
zusammenfällt. Die ganzzahligen Komponenten h,k,l sind die (Millerschen) Indizes von Netzebenen des Abstands d=1/| ![]()
| (| ![]()
| =2sinθ/λ). Jedes Beugungsmaximum ist durch ein Tripel ganzer Zahlen h,k,l charakterisiert. Multiplikation des reziproken Gittervektors:
mit den direkten Basisvektoren ![]()
, ![]()
, ![]()
gibt unter Beachtung der Orthogonalitätsbeziehungen zwischen direkter und reziproker Basis die Laue-Bedingungen:
für das Auftreten von Beugungsmaxima. Röntgenbeugung an Einkristallen kann formal als Reflexion an Netzebenen (h,k,l) beschrieben werden, wobei ![]()
in Richtung der Netzebenennormalen zeigt. Der Winkel 2θ zwischen einfallendem und gebeugtem Röntgenstrahl folgt aus der Braggschen Gleichung (n=Beugungsordnung):
nλ=2d sinθ, n=0,1,2,...,
die als skalare Form der Laue-Bedingungen anzusehen ist.
Um mit monochromatischer Röntgenstrahlung von einem Einkristall Reflexe zu erhalten, muß der Kristall für jeden Reflex in eine solche Orientierung gebracht werden, daß die Laue-Bedingungen erfüllt sind. Es gibt eine Reihe von Apparaturen (Einkristalldiffraktometer), die genau das in systematischer Weise für alle meßbaren Punkte des reziproken Raums ausführen. Alternativ kann man weiße Röntgenstrahlung verwenden, die ein breites Wellenlängenband enthält, aus dem sich der feststehende Kristall die geeigneten Wellenlängen gewissermaßen ›aussucht‹ (Laue-Methode). Die Laue-Bedingungen sind gleichzeitig für viele Reflexe erfüllt, ein Reflex h,k,l und seine höheren Ordnungen fallen allerdings aufeinander. An Stelle von Einkristallen kann man polykristalline Pulverproben verwenden, die aus regellos orientierten Kristalliten (optimale Größe ca. 1 μm) bestehen, um die Beugungsbedingungen (für alle Reflexe gleichzeitig) einzustellen. Die Reflexe einer Pulverprobe liegen auf Beugungskegeln mit Öffnungswinkeln 2θ, die durch das Braggsche Gesetz gegeben sind. Beobachtet werden auf einem konzentrisch um die Probe gelegten Film dann die Schnittgebilde dieser Kegel mit dem Film in Form gekrümmter ›Pulverlinien‹, die man mit Pulverdiffraktometern in Form eines Pulverdiagramms (Zählrate als Funktion von 2θ) erhalten kann. Alle Reflexe mit dem gleichem sinθ/λ fallen aufeinander. Weiße Röntgenstrahlung wird mit Pulver seltener angewendet; energiedispersive Meßtechniken mit stationärer Pulverprobe und energieauflösendem Detektor sind dann von Vorteil, wenn äußere Bedingungen wie Druck und Temperatur variiert werden.
Laue-Bedingungen und Braggsche Gleichung beschreiben geometrische Bedingungen für das Auftreten von Reflexen, deren genaue Position von der Metrik der Elementarzelle abhängt. Informationen über den Elementarzellinhalt und die Elektronendichteverteilung (Elektronendichte) sind nicht in der Position der reziproken Gitterpunkte, sondern in den elastischen Röntgenbeugungsintensitäten I(![]()
) enthalten. Die an Einkristallen gemessene integrale Intensität:
ist in der kinematischen Theorie proportional zum Quadrat der Strukturamplitude (k=Skalenfaktor, L=Lorentzfaktor, P=Polarisationsfaktor, A=Absorptionsfaktor, E=Extinktionsfaktor), wobei der Skalenfaktor k Naturkonstanten, Kristallvolumen, Wellenlänge und Primärintensität enthält. Auch für Kristallpulver ist die integrale Intensität proportional zum Quadrat der Strukturamplitude:
mit k=Skalenfaktor, M=Flächenhäufigkeit, L=Lorentzfaktor, P=Polarisationsafaktor, A=Absorptionsfaktor. Der Absorptionsfaktor A ist für unendlich dicke Proben in der üblichen Meßgeometrie konstant. Die Flächenhäufigkeit M berücksichtigt die Anzahl symmetrisch äquivalenter Reflexe, die jeweils in einer Pulverlinie zusammenfallen. Der Faktor ψ korrigiert gegebenenfalls die Vorzugsorientierung in der Pulverprobe. Ziel einer Röntgenstrukturanalyse ist die Bestimmung der Elektronendichte ρ(![]()
) des Kristalls. Für einen Idealkristall kann diese mathematisch als Faltung der Elektronendichteverteilung ρV(![]()
) einer Elementarzelle mit dem Kristallgitter formuliert werden:
wobei das Gitter durch eine dreidimensional periodische Anordnung von Deltafunktionen δ(u,v,w) mit ganzzahligen Koeffizienten u,v,w dargestellt wird. Das Beugungsmuster wird in der kinematischen Theorie der Röntgenbeugung (Fraunhofer-Beugung) durch die Fouriertransformierte (Fouriertransformation) des streuenden Objekts beschrieben; nach dem Faltungssatz durch das Produkt der Fouriertransformierten des Gitters mit der Fouriertransformierten der Elektronendichte einer Elementarzelle:
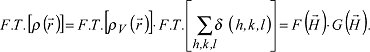
Der Gitterfaktor G(![]()
) gibt die Form eines Interferenzmaximums wieder; der Strukturfaktor F(![]()
) beschreibt die Überlagerung der an den N Atomen (mit Position ![]()
j, Atomformfaktor fj und Temperaturfaktor Tj) der Elementarzelle gestreuten Wellen in Form einer Fourierreihe:
Rücktransformation der Strukturfaktoren gibt wieder die Elektronendichte (V=Elementarzellvolumen):
erfordert allerdings die Kenntnis von Amplitude und Phase aller Strukturfaktoren (Phasenproblem). Zur Strukturbestimmung mit Einkristallen werden hauptsächlich Pattersonsynthesen (Patterson-Funktion), die Technik des isomorphen Ersatzes und Direkte Methoden verwendet. Die daraus erhaltenen Strukturmodelle werden dann in einem weiteren Schritt durch die Strukturverfeinerung optimiert. Pulverdiagramme dienen im wesentlichen zur qualitativen und quantitativen Phasenanalyse sowie zur Verfeinerung nicht zu komplexer Kristallstrukturen mit der Rietveld-Technik, bei der dem gemessenen Pulverdiagramm gemeinsam mit Geräteparametern ein Strukturmodell angepaßt wird ( Abb. 1 u. 2). [KE]
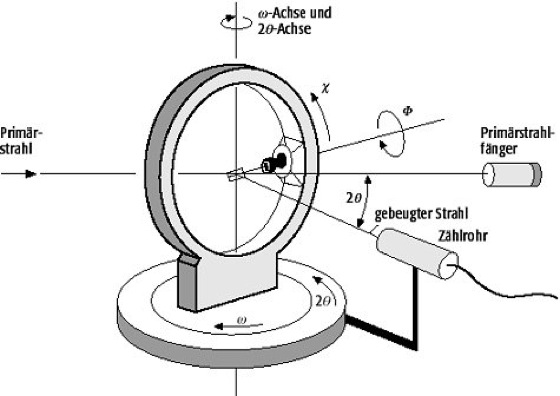
Röntgenstrukturanalyse 1: schematische Skizze eines automatischen 4-Kreis-Diffraktometers mit Eulerwiege. Mit den drei Kreisen ω, χ und Φ kann ein im gemeinsamen Schnittpunkt aller Kreise montierter Einkristall so orientiert werden, daß er für einen bestimmten Reflex h,k,l die Laue-Bedingungen erfüllt. Der vierte Kreis trägt einen Röntgendetektor und wird auf den Winkel 2θ positioniert, der sich für diesen Reflex aus der Braggschen Gleichung ergibt. Zur Aufnahme eines kompletten Datensatzes werden mehrere tausend Reflexe einzeln nacheinander angefahren und ihre integrale Intensität gemessen. Röntgenstrukturanalyse 1:
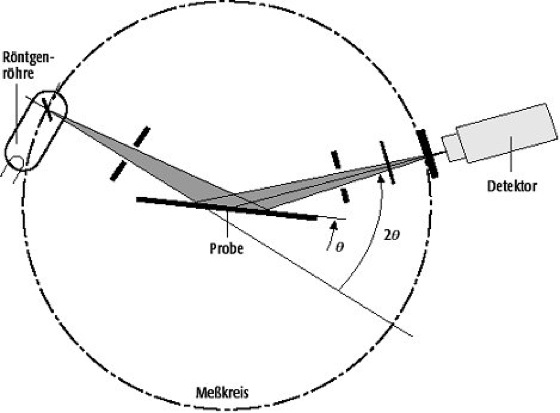
Röntgenstrukturanalyse 2: schematische Skizze eines Pulverdiffraktometers mit Bragg-Brentano-Gemometrie. Die flache Pulverprobe und der Detektor werden im Verhältnis 1:2 gekoppelt bewegt und die Beugungsintensität I(2θi) als Funktion von 2θ schrittweise gemessen. Die Winkelauflösung wird von einer spaltförmigen Eintrittsblende vor dem Detektor bestimmt (typischer Öffnungswinkel: 0,05º). Röntgenstrukturanalyse 2:
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.