Hemmes mathematische Rätsel: Reliefpfeiler
Henry Ernest Dudeney war wohl der bedeutendste Rätselerfinder, der jemals lebte. Es gibt heute kaum ein Denksportaufgabenbuch, das nicht Dutzende seiner Probleme enthält. Aus seinem Buch »The Canterbury Puzzles«, das 1907 in London erschien, stammt das folgende Rätsel.
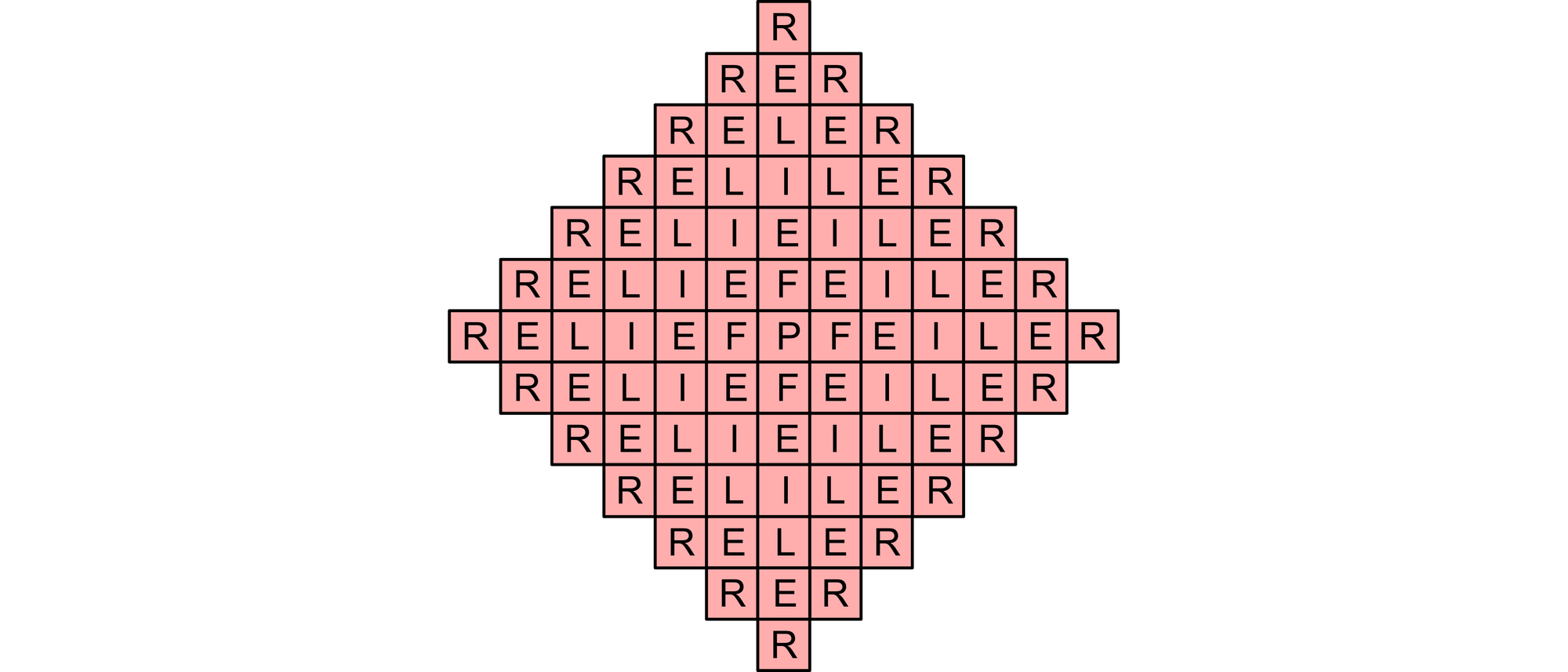
Auf wie vielen verschiedenen Wegen kann ein König auf diesem seltsam geformten Schachbrett das Wort »Reliefpfeiler« nachziehen? Selbstverständlich darf der König nur die beim Schachspiel üblichen Züge machen.
Wir betrachten zunächst nur ein Viertel des Bretts und lassen den König nur das Wortteil »PFEILER« ziehen. Da das »P« nur auf einem Feld vorkommt, muss dort der Weg beginnen. Der König hat nun bei jedem Zug zwei Möglichkeiten, wie er weiter gehen kann. Da er vom »P« aus noch sechs Züge machen muss, sind dies insgesamt 26 = 64 Möglichkeiten.
Jede der vier Reihen des vollständigen Bretts, die vom »P« aus gerade nach links, rechts, oben und unten führen, kann der König an beliebiger Stelle verlassen, aber dann kommt er aus dem Viertel, in das er hineingegangen ist, nicht mehr heraus. Deshalb ist beim vollständigen Brett die Zahl der möglichen Wege, auf denen er »PFEILER« ziehen kann, viermal so groß wie beim Viertelfeld. Allerdings muss man von der Zahl noch wieder 4 abziehen, da man sonst die vier geraden Reihen, die vom »P« ausgehen, doppelt gezählt hat.
Man erhält also insgesamt 4 · 26 − 4 = 252 mögliche Wege. Da »RELIEFP« genau die Umkehrung von »PFEILER« ist, kann der König das Wortteil »RELIEFP« auf genauso vielen Wegen vom Rand zur Mitte ziehen wie das Wortteil »PFEILER« von der Mitte zum Rand. Somit gibt es für den König insgesamt 2522 = 63504 Wege, um das Wort »RELIEFPFEILER« zu bilden.
Schreiben Sie uns!
Beitrag schreiben