Hemmes mathematische Rätsel: Welchen Wert hat der Winkel?
Der 1944 geborene Schweizer Mathematiker Hans Walser hat viele Jahrzehnte lang als Lehrer an Gymnasien und als Lehrbeauftragter an Universitäten unterrichtet. Er hat eine große Zahl von Artikeln und auch etwa ein Dutzend Bücher verfasst. Im Internet betreibt er eine Seite, die er »Miniaturen« nennt. Von dieser Seite stammt die heutige Kopfnuss. Er hat sie im Mai 2022 auf eine Anregung des 1946 geborenen deutschen Grafikers, Designers und Malers Jo Niemeyer hin entworfen.
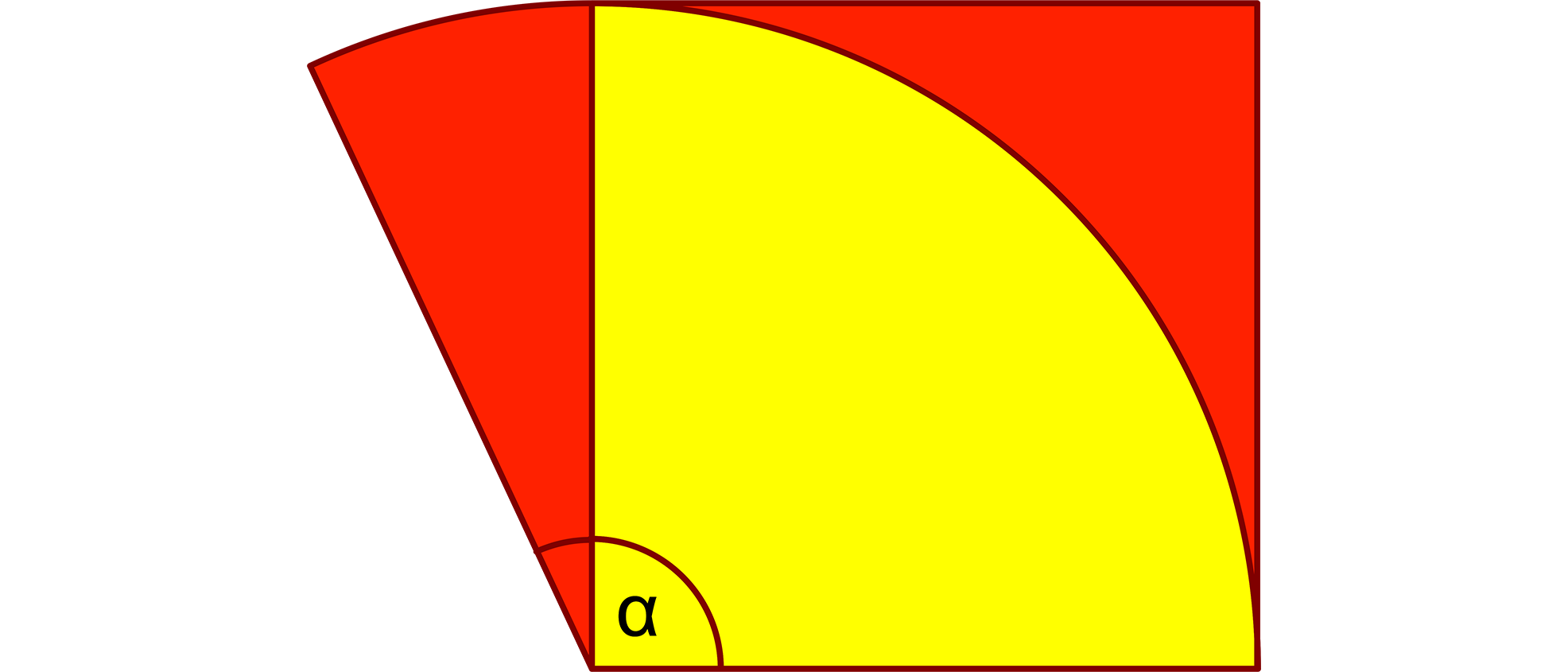
„Einfache“ Winkel wie ein gestreckter Winkel, ein rechter Winkel und ein Sechstelvollwinkel haben im Gradmaß die ganzzahligen Werte 180°, 90° und 60°. Im Bogenmaß hingegen sind ihre Werte die unschönen Zahlen 3,1415…, 1,5707… und 1,0471… mit unendlich vielen Nachkommastellen. Darum gibt man sie in der Regel als Vielfache der Kreiszahl an: π, 1/2π und 1/3π. Der Wert des Winkels α in dieser Aufgabe ist jedoch eine Ausnahme vom Üblichen. Die beiden roten Flächen, die von Kreisbögen und Quadratseiten begrenzt werden, sind gleich groß. Welchen Wert hat der Winkel α im Bogenmaß?
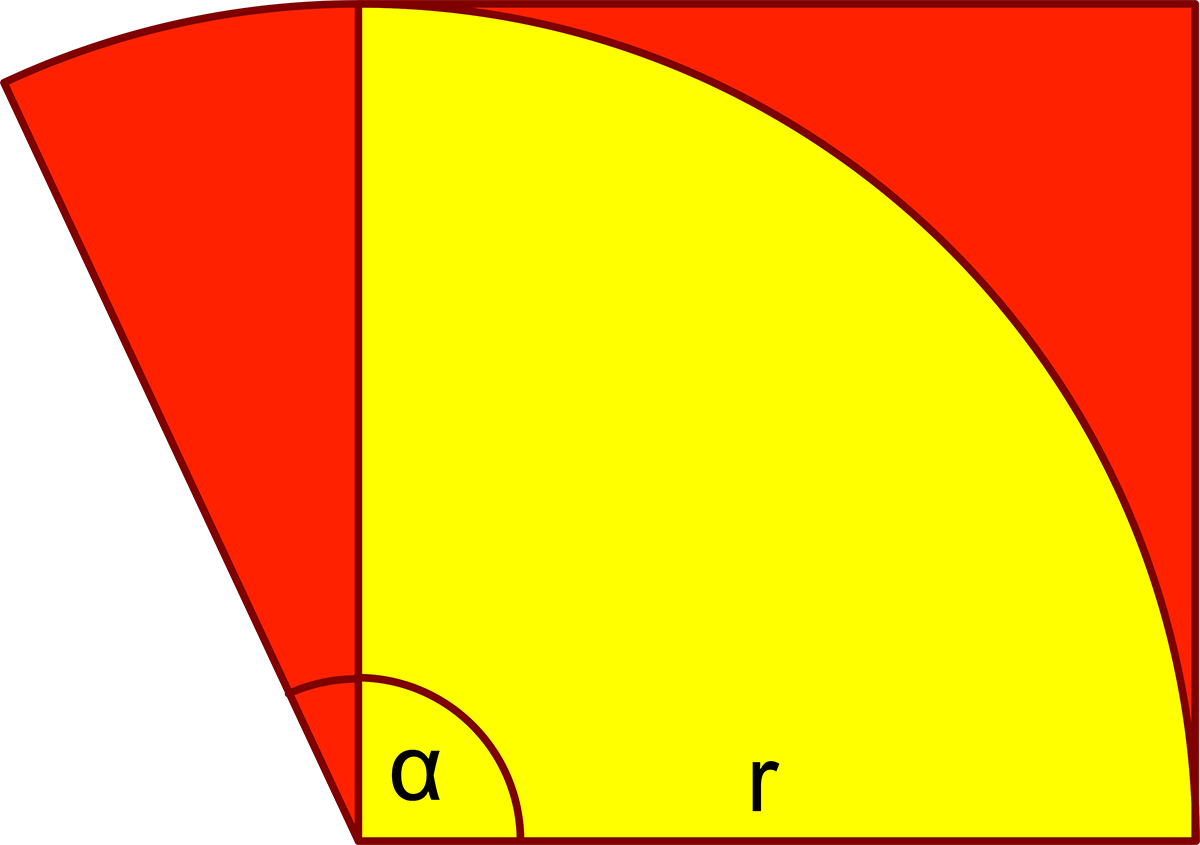
Die beiden roten Flächen sind gleich groß. Darum muss der Kreisausschnitt mit dem Winkel α, der sich aus dem roten Kreisausschnitt und dem gelben Viertelkreis zusammensetzt, den gleichen Inhalt haben wie das Quadrat. Ist r der Radius der Kreisbögen und die Seitenlänge des Quadrats, gilt für die Inhalte des Kreisausschnitts und des Quadrats απr2/(2π) = r2, was sich zu α = 2 umformen lässt. Dieser Winkel, dessen Größe im Bogenmaß eine natürliche Zahl ist, hat im Gradmaß den unschönen Wert 2 ∙ 180°/π = 114,5915…°.









Schreiben Sie uns!
Beitrag schreiben