Hemmes mathematische Rätsel: Welcher Wert ist gesucht?
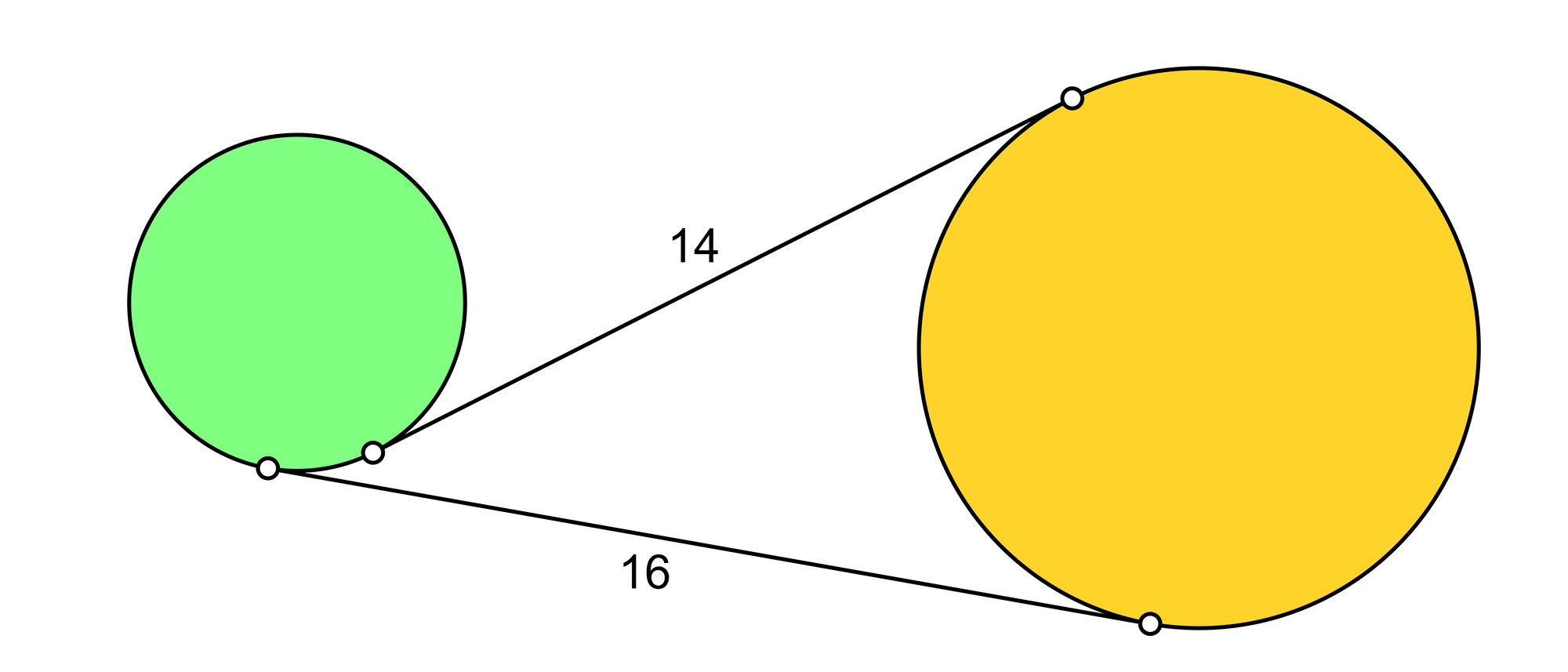
Das Bild zeigt zwei Kreise mit zwei gemeinsamen Tangenten, die die Längen 14 und 16 haben. Wie groß ist der Flächeninhalt eines Rechtecks, dessen Seiten so lang sind wie die Radien der beiden Kreise?
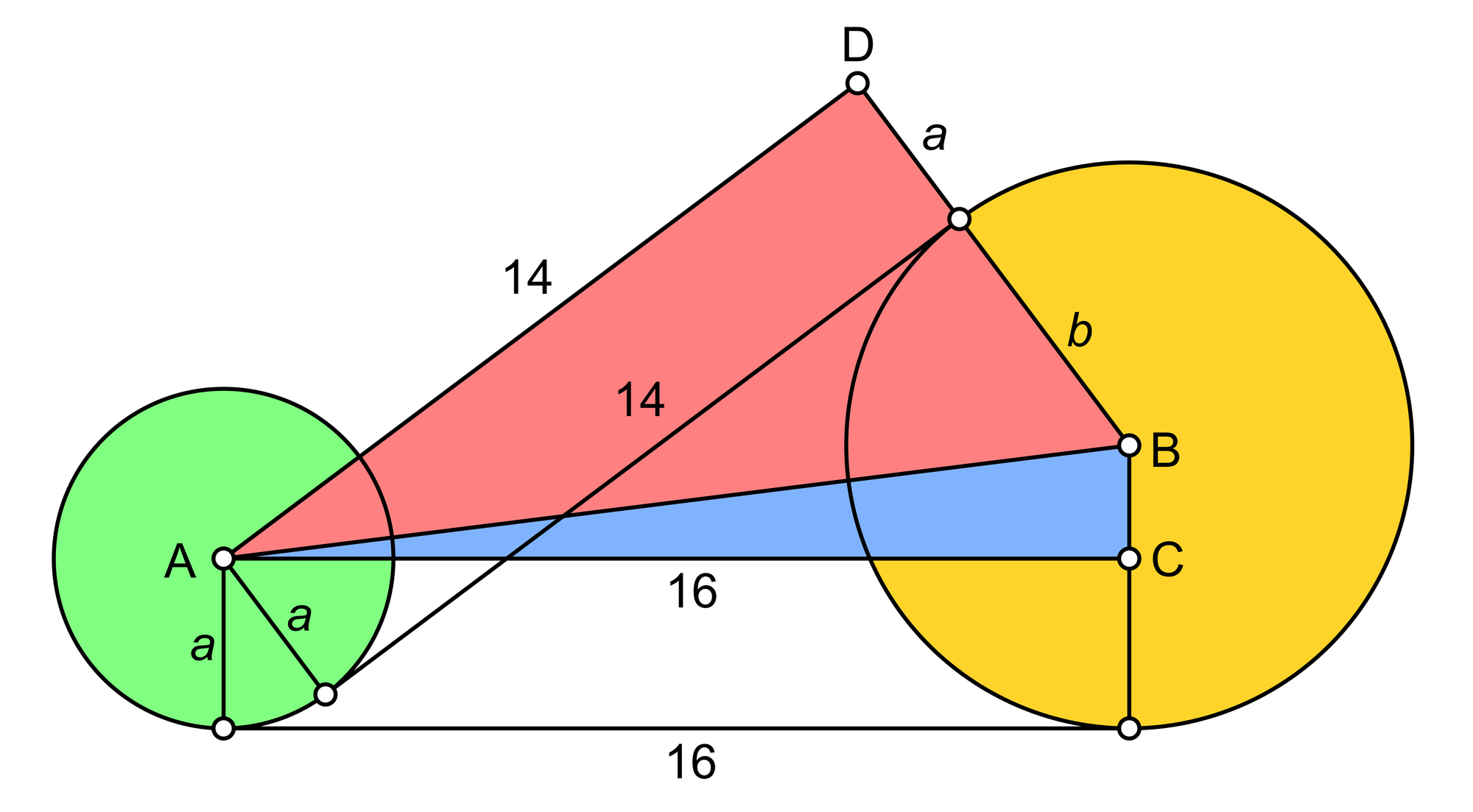
Haben die beiden Kreise die Mittelpunkte A und B und die Radien a und b, so haben die Katheten des blauen rechtwinkligen Dreiecks ABC die Längen 16 und b – a und die Katheten des roten rechtwinkligen Dreiecks ABD die Längen 14 und b + a. Für die gemeinsame Hypotenuse AB der beiden Dreiecke gilt somit nach dem Satz des Pythagoras (AB)2 = 162 + (b – a)2 = 142 + (b + a)2. Die zweite Gleichung dieser Doppelgleichung lässt sich zu 162 – 142 = (b + a)2 – (b – a)2 oder (16 – 14)(16 + 14) = ((b + a) – (b – a))((b + a) + (b – a)) umformen. Dies ergibt 2 · 30 = 2a · 2b oder ab = 15. Der Flächeninhalt eines Rechtecks, dessen Seiten so lang sind wie die Radien a und b der beiden Kreise, beträgt folglich 15.









Schreiben Sie uns!
Beitrag schreiben