Hemmes mathematische Rätsel: Wie groß ist der Radius?
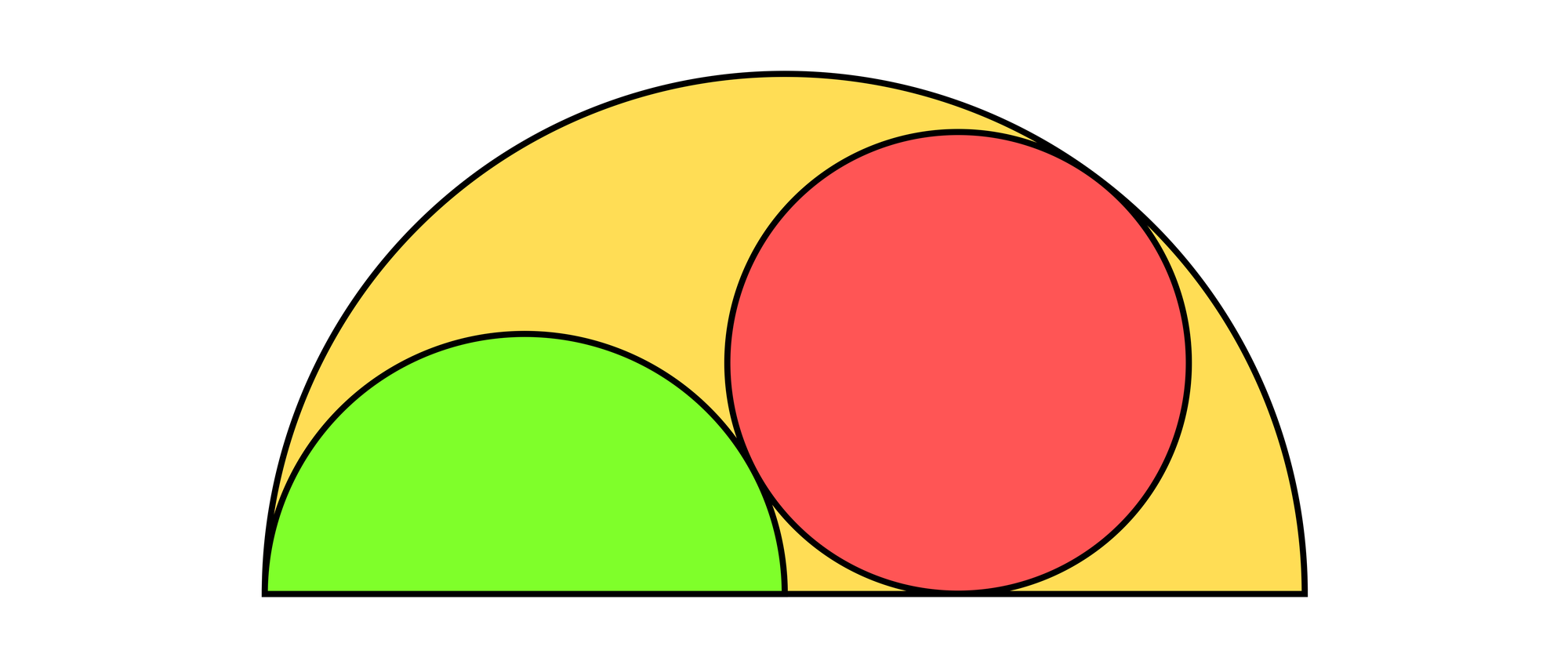
In einem Halbkreis vom Radius 18 liegen ein Halbkreis vom Radius 9 und ein Vollkreis. Wie groß ist der Radius des Vollkreises?
Die Mittelpunkte der beiden Halbkreise und des Vollkreises sind A, B und C, und ihre Radien haben die Längen 18, 9 und r. Folglich gilt für die Strecken BC = 9 + r und AQ = 18 und AC = 18 – r. Bezeichnen wir die Strecke AP mit x, so bekommt man für das rechtwinklige Dreieck APC nach dem Satz des Pythagoras x2 + r2 = (18 – r)2, was man zu 36r = 324 – x2 vereinfachen kann. Auch auf das Dreieck BPC wird der Satz des Pythagoras angewendet, und man erhält (9 + x)2 + r2 = (9 + r)2 oder 36x + 2x2 = 36r. Setzt man die beiden Ausdrücke für 36r gleich, erhält man 36x + 2x2 = 324 – x2 oder x2 + 12x – 108 = 0. Die positive Lösung dieser quadratischen Gleichung ist x = 6, woraus sich dann auch sofort r = 8 ergibt.
Schreiben Sie uns!
Beitrag schreiben