Hemmes mathematische Rätsel: Welcher Wert ist gesucht?

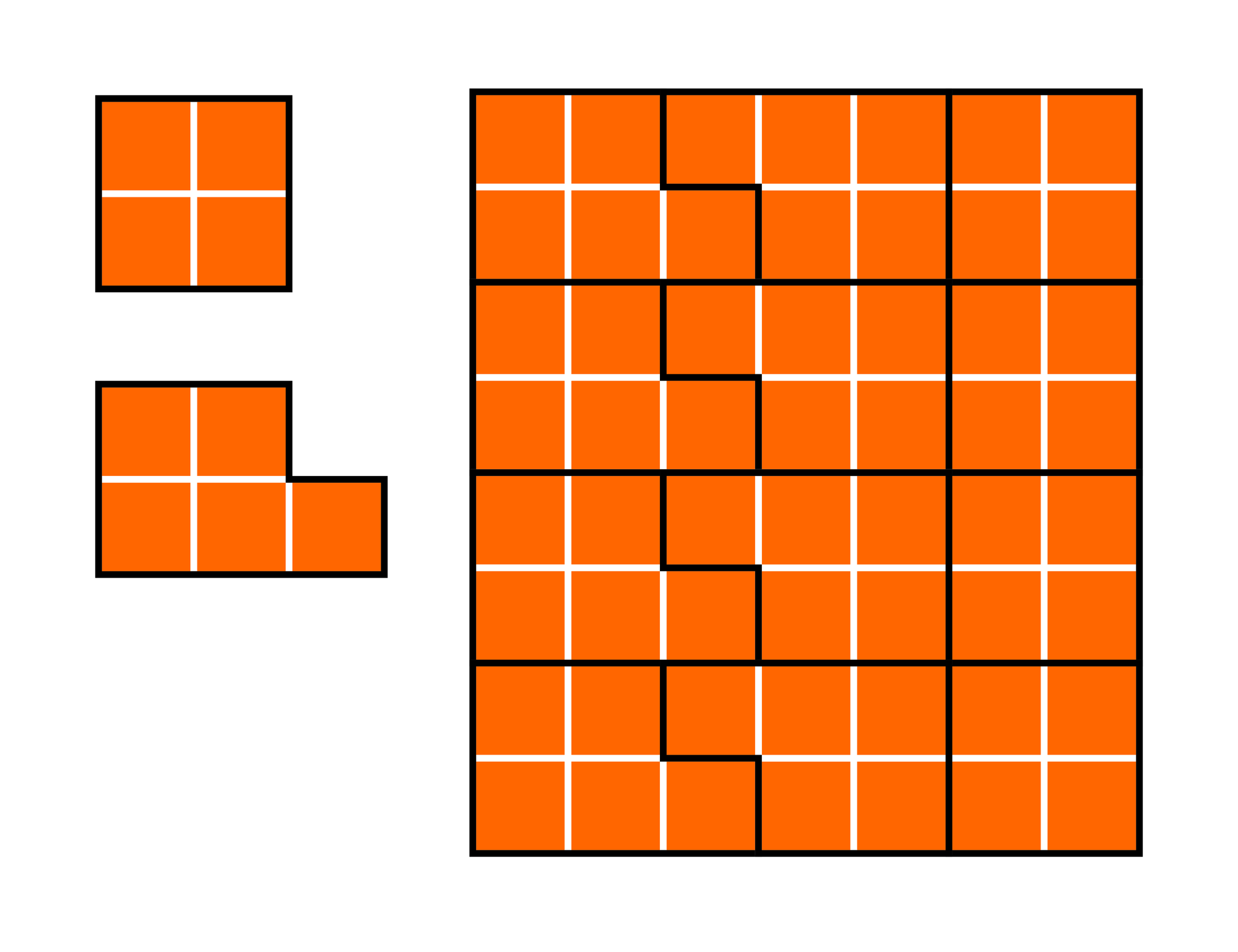
Zerschneiden Sie dieses 7×8-feldige Schachbrett entlang der Feldgrenzen in einige Polygone, von denen keines aus mehr als fünf Feldern bestehen darf. Außerdem soll die Gesamtlänge aller Schnitte so kurz wie möglich sein. Wie lang ist diese kürzeste Gesamtschnittlänge?

Da die Gesamtlänge aller Schnittlinien möglichst kurz sein soll, muss die Zahl aller Feldgrenzen, die nicht Teil einer Schnittlinie sind, möglichst groß sein. Bestimmt man von jedem der 21 verschiedenen Polygone, die aus höchstens fünf Feldern bestehen, das Verhältnis der Zahl der Feldgrenzen in seinem Inneren zur Zahl seiner Felder, findet man nur bei den beiden abgebildeten Polygonen ein Verhältnis von 1. Bei allen anderen Polygonen ist es kleiner. Zerschneidet man das Schachbrett also in diese Polygone, wird die Gesamtschnittlänge minimal. Das Bild zeigt ein Beispiel dafür. Haben die Felder die Seitenlänge 1, so beträgt die Gesamtschnittlänge 41.









Schreiben Sie uns!
Beitrag schreiben