Hemmes mathematische Rätsel: Welches Zahlensystem ist gesucht?

Die Mitglieder der mathematischen Gesellschaft der altehrwürdigen englischen Universität Cambridge haben sich den klangvollen Namen „Archimedier“ gegeben. Seit 1939 geben sie etwa einmal pro Jahr eine Zeitschrift mit dem Titel „Eureka“ heraus. In ihr veröffentlichen Studenten und Mathematiker aus der ganzen Welt Artikel aus allen Bereichen der Mathematik, aber auch über Denksportaufgaben und Puzzles. Viele berühmte Mathematiker und Physiker haben für „Eureka“ Aufsätze geschrieben. In der im Oktober 1960 herausgegebenen 23. Ausgabe von „Eureka“ stellten G. J. S. Ross und M. Westwood folgendes Rätsel.
Unter einer Alphametik versteht man eine korrekte Rechnung, bei der die Zahlen durch Wörter ersetzt worden sind. Jeder Buchstabe steht dabei für eine Ziffer. Gleiche Buchstaben bedeuten auch gleiche Ziffern, und verschiedene Buchstaben stehen für verschiedene Ziffern. Keine Zahl darf mit einer 0 beginnen.
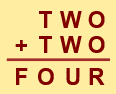
Sind TWO und FOUR Zahlen des Dezimalsystems, also des Zahlensystems mit der Basis 10, hat die Alphametik sieben verschiedene Lösungen. Wählt man Zahlensysteme mit kleineren Basen, sinkt die Zahl der Lösungen. Welches ist das Zahlensystem mit der kleinsten Basis, in dem die Alphametik überhaupt noch Lösungen hat, und wie lauten diese Lösungen?
Da in der Alphametik sechs verschiedene Buchstaben und damit auch Ziffern vorkommen, muss die Basis b mindestens 6 sein. Addiert man zwei Ziffern einer Spalte der Alphametik und den eventuellen Übertrag von 1 aus der Vorgängerspalte, kann die Summe s nur ein- oder zweistellig sein. Sie ist einstellig, wenn s < b ist, und man sieht dann keinen Unterschied zum Dezimalsystem. Für s ≥ b ist sie hingegen zweistellig, und die erste Stelle ist eine 1 und die zweite Stelle beträgt s – b. Unabhängig von der Basis b muss F = 1 sein. Aus der letzten Spalte folgt, dass O nicht 0 sein kann, da R dann auch 0 sein müsste. Wenn O = b – 1 wäre, müsste in der zweiten Spalte auch T = b – 1 sein, damit es einen Übertrag auf die erste Spalte gibt. Das ist aber unmöglich, somit kann O nur 2, 3 … oder b – 2 sein. Nehmen wir zunächst einmal b = 6 an. Dann kann O nur 2, 3 oder 4 sein. Probiert man jeden der drei Fälle durch, gelangt man jedes Mal zu einem Widerspruch. Also ist b ≠ 6. Bei b = 7 kann O = 2, 3, 4 oder 5 sein. Probiert man auch diese Fälle durch, findet man nur für O = 3 eine Lösung. Folglich ist die kleinste Basis b = 7 und die einzige Lösung von TWO + TWO = FOUR für diese Basis 523 + 523 = 1346.









Schreiben Sie uns!
Beitrag schreiben