Hemmes mathematische Rätsel: Wie groß ist der Durchmesser des Umkreises?
2021 stellte Manfred Pietsch aus Kreuzau den Leserinnen und Lesern der »Aachener Zeitung« und der »Aachener Nachrichten« ein hübsches kleines geometrisches Problem.
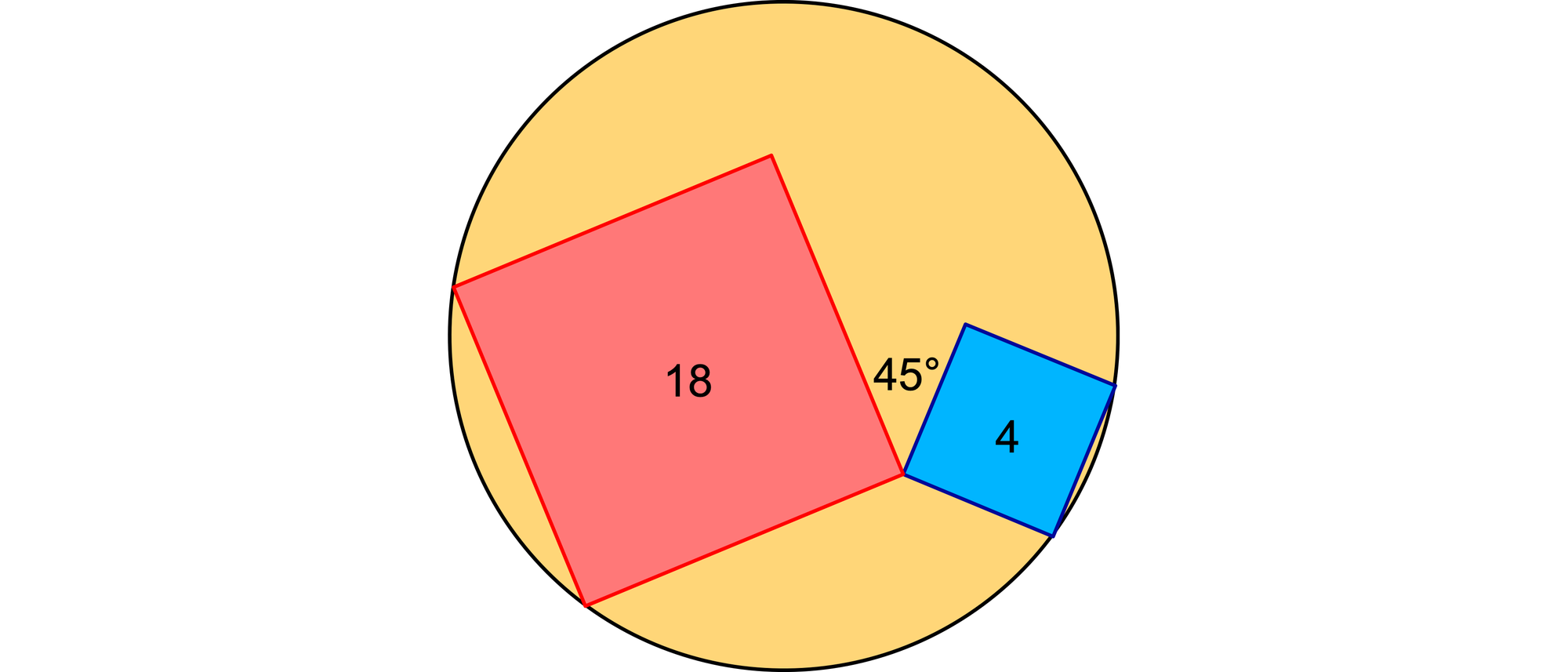
Zwei Quadrate mit den Flächeninhalten 18 und 4 haben einen gemeinsamen Eckpunkt und schließen dort einen Winkel von 45° ein. Die Figur wird von einem Kreis umschlungen, auf dem je zwei Ecken beider Quadrate liegen. Wie groß ist der Durchmesser dieses Umkreises?
Die Diagonale PA des blauen Quadrats schließt mit den benachbarten Quadratseiten Winkel von α = 45° ein. Da auch die beiden Quadrate am Punkt P einen Winkel von 45° einschließen, stehen die Strecken PQ und PA senkrecht aufeinander, und die drei Punkte A, P und C liegen auf einer Geraden.
Folglich ist das Dreieck ABC rechtwinklig und seine Hypotenuse AB nach dem Satz des Thales ein Kreisdurchmesser. Mit BC = CP = √18 und PA = 2√2 ergibt sich für das Dreieck ABC nach dem Satz des Pythagoras (AB)2 = (√18)2 + (√18 + 2√2)2, was sich zu AB = 2√17 ≈ 8,246 vereinfachen lässt.
Schreiben Sie uns!
5 Beiträge anzeigen