Hemmes mathematische Rätsel: Wie groß ist die Dachfläche?
2021 stellte Manfred Pietsch aus Kreuzau in Nordrhein-Westfalen in den »Aachener Nachrichten« und in der »Aachener Zeitung« ein seltsames Gebäude vor.
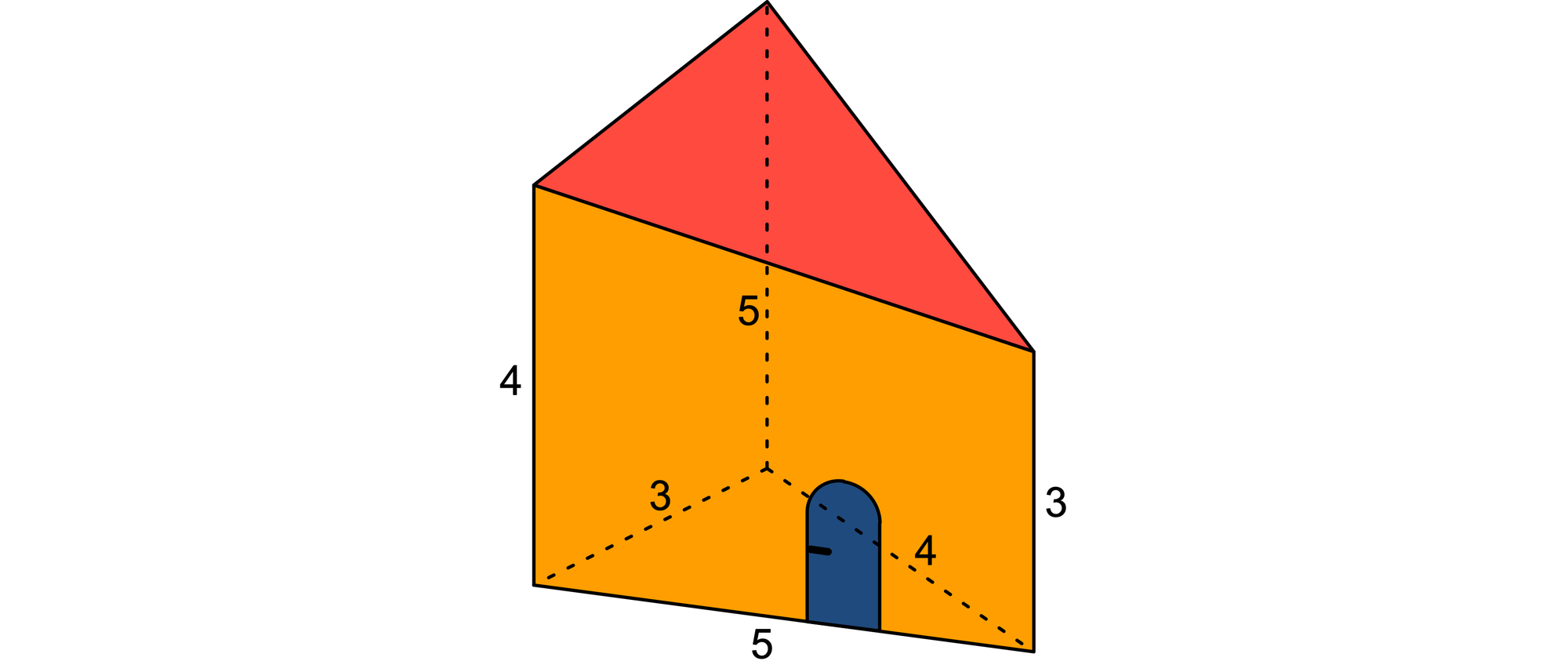
Die Schildbürger errichteten in ihrer Stadt ein fensterloses Rathaus von ungewöhnlicher Form. Seine Grundfläche war ein Dreieck mit 3, 4 und 5 Ruten Seitenlänge. Auch die drei senkrechten Kanten des Rathauses waren 3, 4 und 5 Ruten hoch. Die Schildbürger, die berühmt sind für ihre Weisheit und für ihre Liebe zur Mathematik, ordneten die Kanten so an, dass an jeder Hausecke drei Kanten unterschiedlicher Längen zusammentrafen.
Im Rathaus war es dunkel, und da sie Licht für ein Element wie Wasser hielten, versuchten sie, es, wenn auch erfolglos, mit Eimern hineinzutragen. Das Dach des Rathauses war flach und auch ein Dreieck, aber es war geneigt, so dass das Regenwasser an einer Ecke ablaufen konnte.
Wissen Sie, wie groß die Dachfläche war?
Jede der drei trapezförmigen Rathauswände kann man durch eine Parallele zum Erdboden in ein Rechteck und ein rechtwinkliges Dreieck teilen.
Die drei rechtwinkligen Dreiecke lassen sich zu einem Rechteck anordnen, bei dem die Hypotenusen im Inneren die freie dreieckige, rote Fläche A begrenzen. Da A die gleichen Seitenlängen hat wie das Rathausdach, sind die beiden Flächen gleich. Somit ist die Dachfläche die Differenz zwischen der Rechteckfläche und der Gesamtfläche der drei rechtwinkligen Dreiecke: A = 3 · 5 − (1 · 3 + 2 · 4 + 1 · 5)/2 = 7 Quadratruten.
Schreiben Sie uns!
Beitrag schreiben