Hemmes mathematische Rätsel: Wie groß ist x?
© Heinrich Hemme (Ausschnitt)
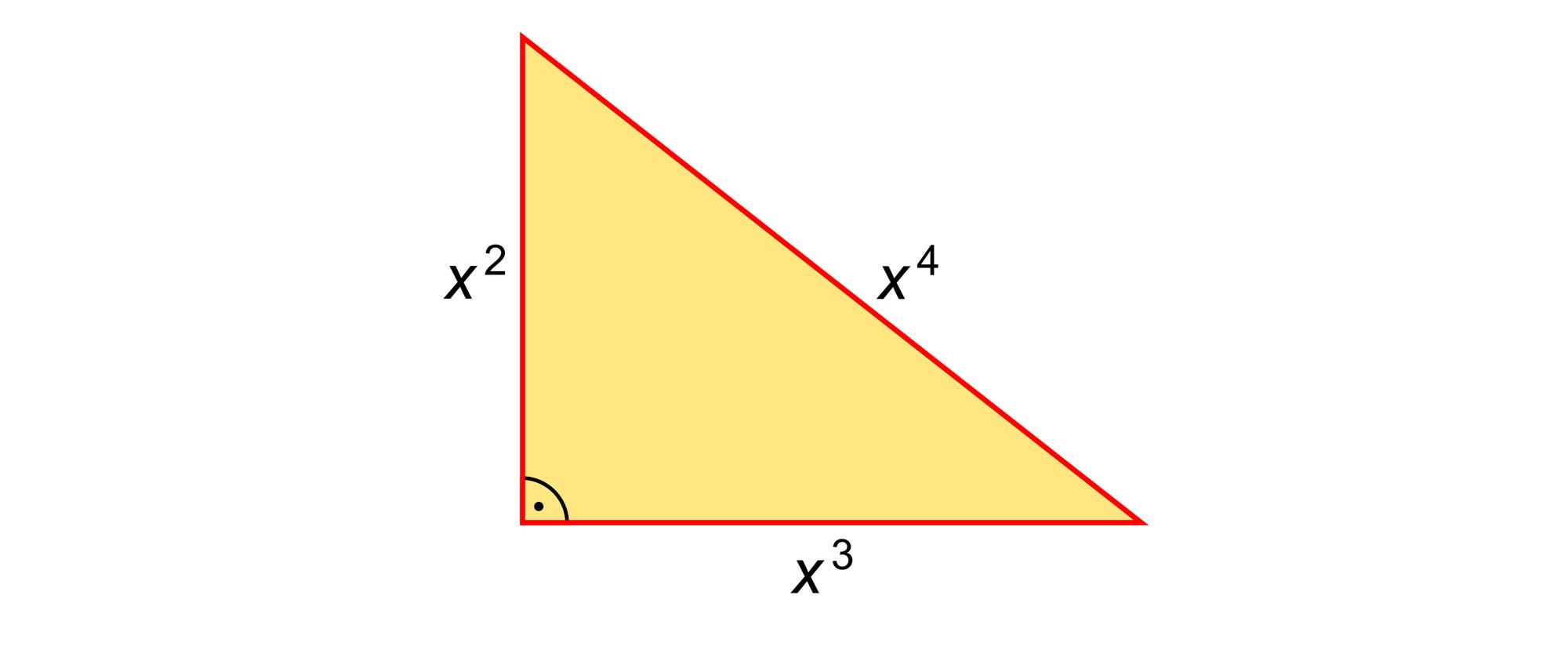
Die Katheten und die Hypotenuse eines rechtwinkligen Dreiecks haben die Längen x2, x3 und x4. Wie groß ist x? Natürlich ist das Dreieck nicht zu einem Punkt entartet.
Nach dem Satz des Pythagoras gilt (x2)2 + (x3)2 = (x4)2, was man auch als x4 + x6 = x8 schreiben kann. Da x ≠ 0 ist, kann man die Gleichung zu 1 + x2 = x4 oder zu x4 – x2 – 1 = 0 vereinfachen. Diese biquadratische Gleichung hat die Lösungen x2 = ½(1 ± √5). Da x2 positiv sein muss, scheidet die negative Lösung aus. Folglich ist x2 = ½(1 + √5). Dies ist der berühmte Goldene Schnitt Φ. Somit ist x = √Φ ≈1,27202.
Schreiben Sie uns!
Beitrag schreiben