Hemmes mathematische Rätsel: Wie groß ist die rote Fläche?
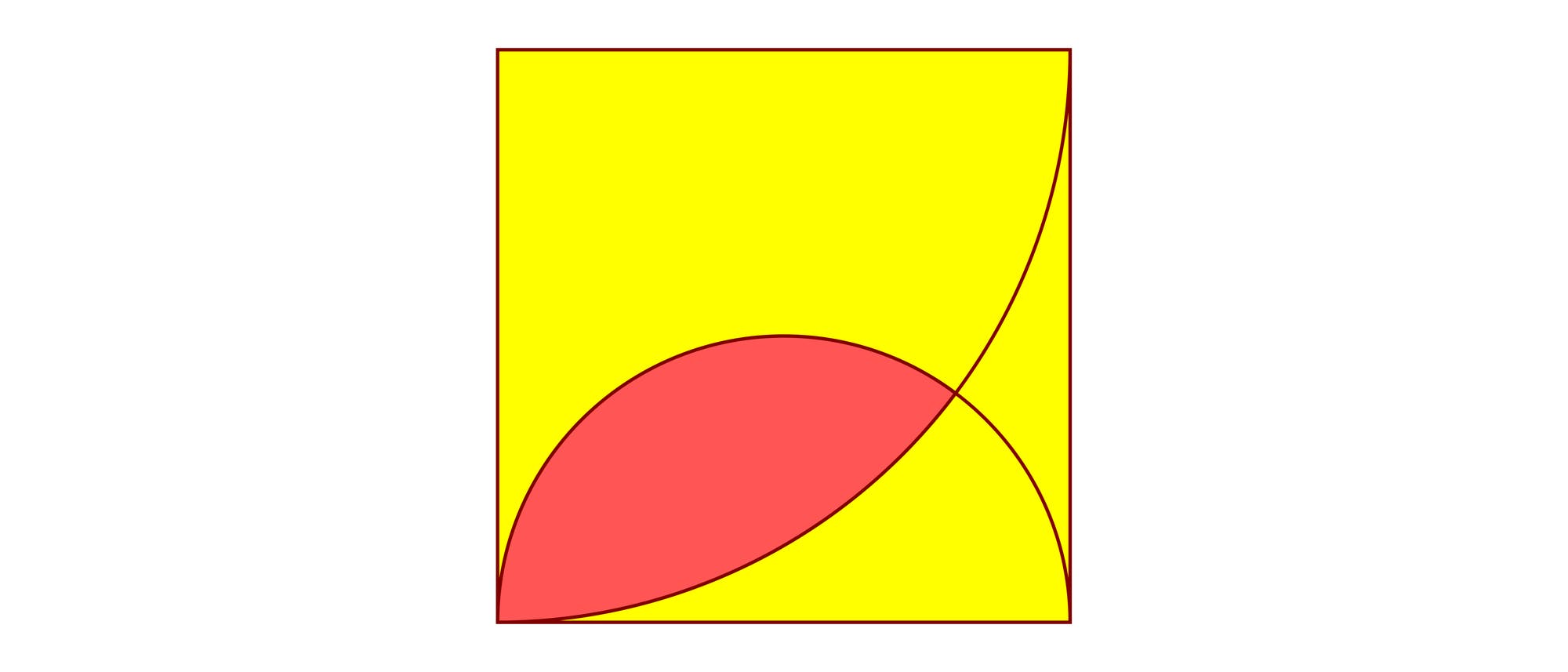
In einem Quadrat der Seitenlänge 2 liegen ein Viertelkreis und ein Halbkreis, so wie es das Bild zeigt. Wie groß ist die rote Fläche?
Der Kreisausschnitt ABF mit dem Radius R = 2 und der Kreisausschnitt EFB mit dem Radius r = 1 decken das Drachenviereck ABEF vollständig ab, wobei sie sich in der roten Fläche überlappen. Der Inhalt X der roten Fläche ist der Inhalt des Kreisausschnitts ABF plus dem Inhalt des Kreisausschnitts EFB minus dem Inhalt des Vierecks ABEF. Das Drachenviereck besteht aus den beiden kongruenten rechtwinkligen Dreiecken ABE und AEF. Sie haben Katheten der Längen R und r und darum zusammen den Flächeninhalt 2 · ½Rr = Rr = 2. Ihre Winkel an der Ecke A haben die Größe α = arctan½. Folglich besitzt der Kreisausschnitt ABF einen Flächeninhalt von 2α/(2π) · πR2 = arctan½ · R2 = 4arctan½. Die beiden Winkel FEA und AEB haben die Größe π/2 – α. Folglich hat der Kreisausschnitt EFB einen Flächeninhalt von 2(π/2 – arctan½)/(2π) · πr2 = (π/2 – arctan½) · r2 = π/2 – arctan½. Damit hat die rote Fläche den Inhalt X = 4arctan½ + π/2 – arctan½ – 2 = 3arctan½ + π/2 – 2 ≈ 0,9617.
Schreiben Sie uns!
Beitrag schreiben