Hemmes mathematische Rätsel: Wie lang ist der kürzeste Weg?
Henry Ernest Dudeney (1857–1930) war wohl der bedeutendste Rätselerfinder, der jemals lebte. Im »Strand Magazine« veröffentlichte er 1914 das folgende Problem.
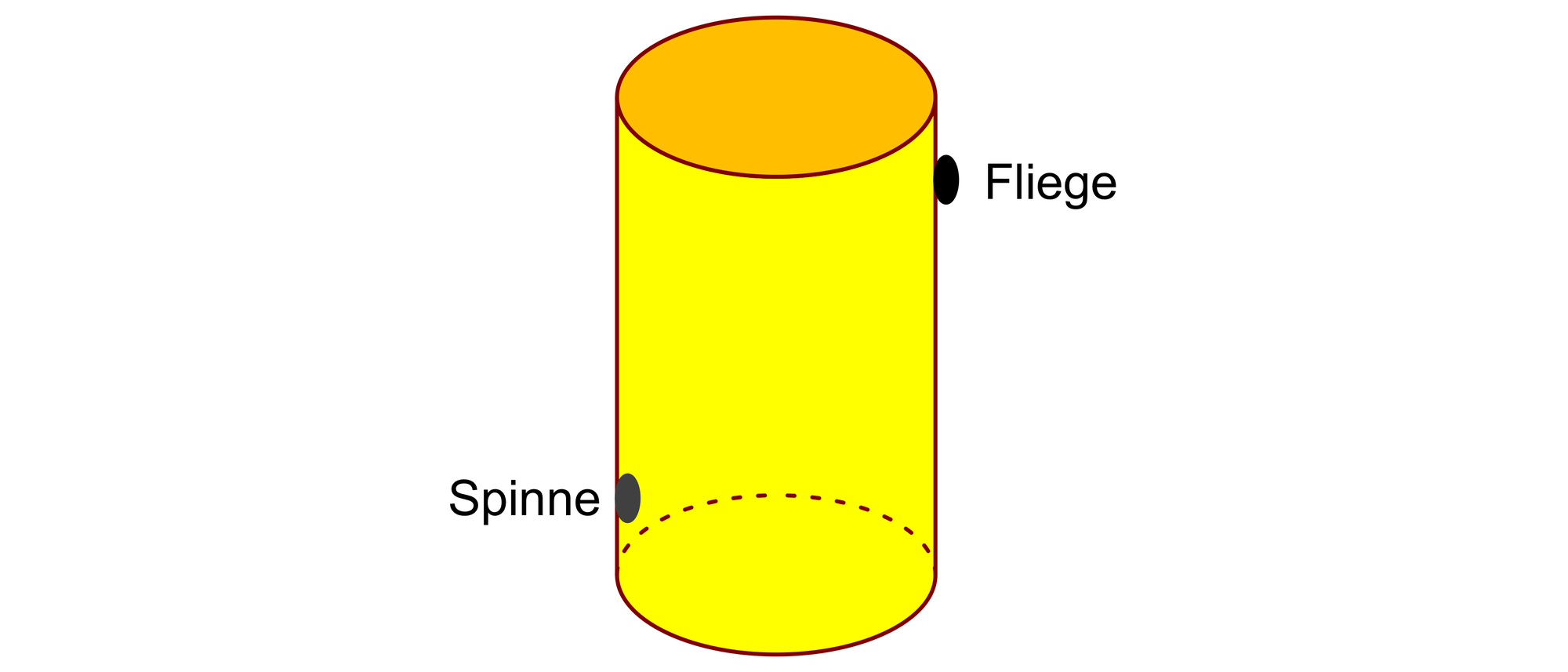
An einem zylinderförmigen Altbierglas, das eine Höhe von 16 cm und einen Umfang von 24 cm hat, sitzt auf der Innenseite, genau 2 cm über dem Boden, eine Spinne. Auf der diametral gegenüberliegenden Seite hat sich 2 cm vom oberen Rand entfernt auf der Außenseite des Glases eine Fliege niedergelassen. Die Spinne will die Fliege fressen und sie deshalb auf dem kürzesten Weg erreichen.
Welchen Weg muss die Spinne nehmen? Wie lang ist er? Die Wandstärke des Glases kann man dabei vernachlässigen.
Um dieses Problem möglichst einfach zu lösen , entfernt man im Gedanken den Boden des Altbierglases, schneidet die übriggebliebene Röhre an einer Stelle auf und wickelt sie zu einer ebenen Glasscheibe ab. Es entsteht so ein Rechteck, dessen eine Seite die Höhe und dessen andere der Umfang des Glases ist.
Dieses Rechteck kann man noch flach durchspalten und entlang seines oberen Randes auseinanderklappen und so Außen- und Innenseite des Glases trennen. Jetzt kann man den kürzesten Weg der Spinne zur Fliege leicht erkennen: Es ist die Gerade durch beide Aufenthaltsorte. Die Entfernung lässt sich mit dem Satz des Pythagoras zu x = √((16 cm)2 + (12 cm)2) = 20 cm berechnen.
Schreiben Sie uns!
Beitrag schreiben