Hemmes mathematische Rätsel: Zwei Würfel
2019 dachte sich Manfred Pietsch aus Kreuzau eine hübsche Aufgabe mit zwei Würfeln aus, die im selben Jahr in der »Aachener Zeitung« und in den »Aachener Nachrichten« erstmals veröffentlicht wurde.
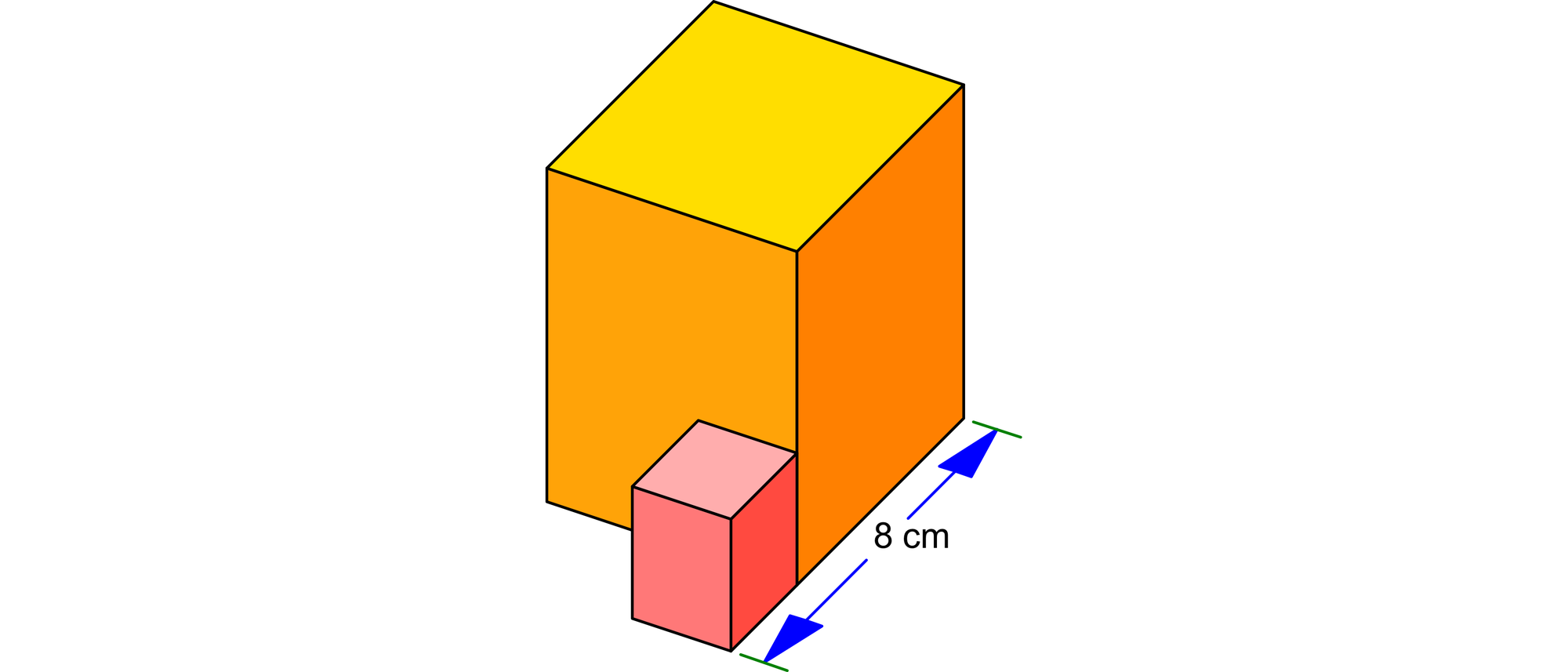
Zwei Würfel liegen nebeneinander so auf dem Tisch. Sie haben zusammen eine Breite von 8 cm und zusammen einen Rauminhalt von 200 cm3. Wie groß ist die gesamte Grundfläche, mit der die beiden Würfel auf der Tischplatte liegen?
Haben die beiden Würfel die Kantenlängen a und b, so haben sie eine Gesamtbreite von a + b = 8 und ein Gesamtvolumen von a3 + b3 = 200. Sie decken zusammen eine Grundfläche von a2 + b2 ab. Natürlich könnte man aus den ersten beiden Gleichungen a und b ermitteln. Doch dabei erhält man hässliche Wurzeln und irrationale Längen.
Diese kann man aber leicht vermeiden, da (a + b)3 = a3 + 3a2b + 3ab2 + b3 = a3 + b3 + 3ab(a + b) ist. Setzt man in diese Gleichung a3 + b3 = 200 und a + b = 8 ein, vereinfacht sie sich zu 83 = 200 + 3ab · 8, was sich zu ab = 13 umformen lässt. Nun ist aber (a + b)2 = a2 + 2ab + b2 = a2 + b2 + 2ab, was mit a + b = 8 und ab = 13 zu 82 = a2 + b2 + 2 · 13 führt. Diese Gleichung kann man zur gesuchten Lösung a2 + b2 = 38 umformen. Die gemeinsame Grundfläche der beiden Würfel beträgt somit 38 cm2.
Schreiben Sie uns!
Beitrag schreiben