Hemmes mathematische Rätsel: Das Zwölfeck
Der Mathematiker Norman Herbert Anning (1883–1963) hat zahlreiche mathematische Knobeleien entworfen und veröffentlicht. 1954 stellte er im »Mathematics Magazine« den Lesern folgende Aufgabe:
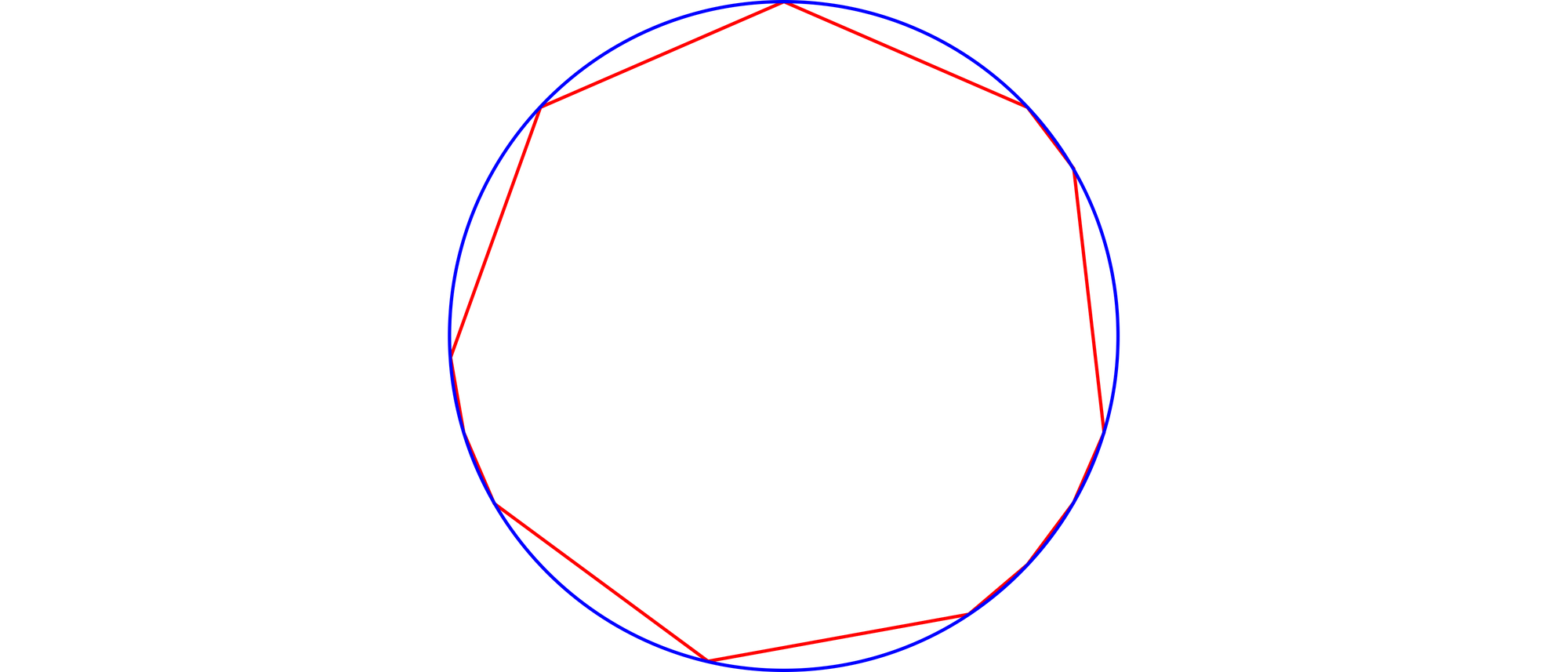
Ein Zwölfeck, dessen Ecken alle auf dem Umfang eines Kreises liegen, hat je sechs Seiten der Längen √2 und √24. Die Reihenfolge der √2 langen und der √24 langen Seiten ist beliebig. Die Zeichnung zeigt ein Beispiel dafür. Welchen Radius hat der Kreis in Abhängigkeit von der Reihenfolge der verschieden langen Seiten?
Wir nehmen einmal an, AB und BC seien zwei benachbarte, aber verschieden lange Seiten des Zwölfecks. Da die Bögen über allen sechs langen und sechs kurzen Seiten zusammen einen Vollkreis bilden, muss der Bogen über eine lange und eine kurze Seite gerade einen Sechstelkreis ergeben. Der Winkel AMC beträgt folglich 360°/6 = 60°. Daraus ergibt sich, das Dreieck AMC muss gleichseitig sein, und die Strecke AC hat die Länge des Kreisradius.
Bezeichnen wir den Winkel AMB mit α, betragen von dem gleichschenkligen Dreiecks AMB die beiden anderen Winkel MAB = MBA = 1⁄2(180° − α) = 90° − 1⁄2α. Der Winkel BMC muss 60° − α sein, und folglich haben in dem Dreieck BMC die beiden anderen Winkel die Werte MBC = MCB = 1⁄2(180° − (60° − α)) = 60° + 1⁄2α. Da der Winkel ABC sich aus den Winkeln MBA und MBC zusammensetzt, beträgt er ABC = MBA + MBC = 90° − 1⁄2α + 60° + 1⁄2α = 150°. Zum Schluss wendet man auf das Dreieck ABC den Kosinussatz an: (AC)2 = (AB)2 + (BC)2 − 2 · AB · BC · cos150°. Setzt man die Werte ein, erhält man (AC)2 = (√2)2 + (√24)2 + 2 · √2 · √24 · 1⁄2√3 = 38. Der Radius des Kreises beträgt also, unabhängig von der Reihenfolge der kurzen und langen Seiten, r = √38 ≈ 6,164.
Der Kosinussatz, den ich hier verwendet habe, ist leider aus den Lehrplänen vieler Schulen verschwunden, dabei ist er sehr nützlich. Er besagt, dass für ein beliebiges Dreieck mit den Innenwinkeln α, β und γ und den den Winkeln gegenüberliegenden Seiten a, b und c stets c2 = a2 + b2 − 2ab cos γ gilt.
Schreiben Sie uns!
Beitrag schreiben