Hemmes mathematische Rätsel: Münzdreiecke
Kobon Fujimura (1903–1983) war einer der bedeutensten Puzzleexperten Japans. Von seinen zahlreichen Denksportaufgabenbüchern ist nur ein einziges in eine westliche Sprache übersetzt worden. Aus einem seiner Bücher stammt das folgende Problem:
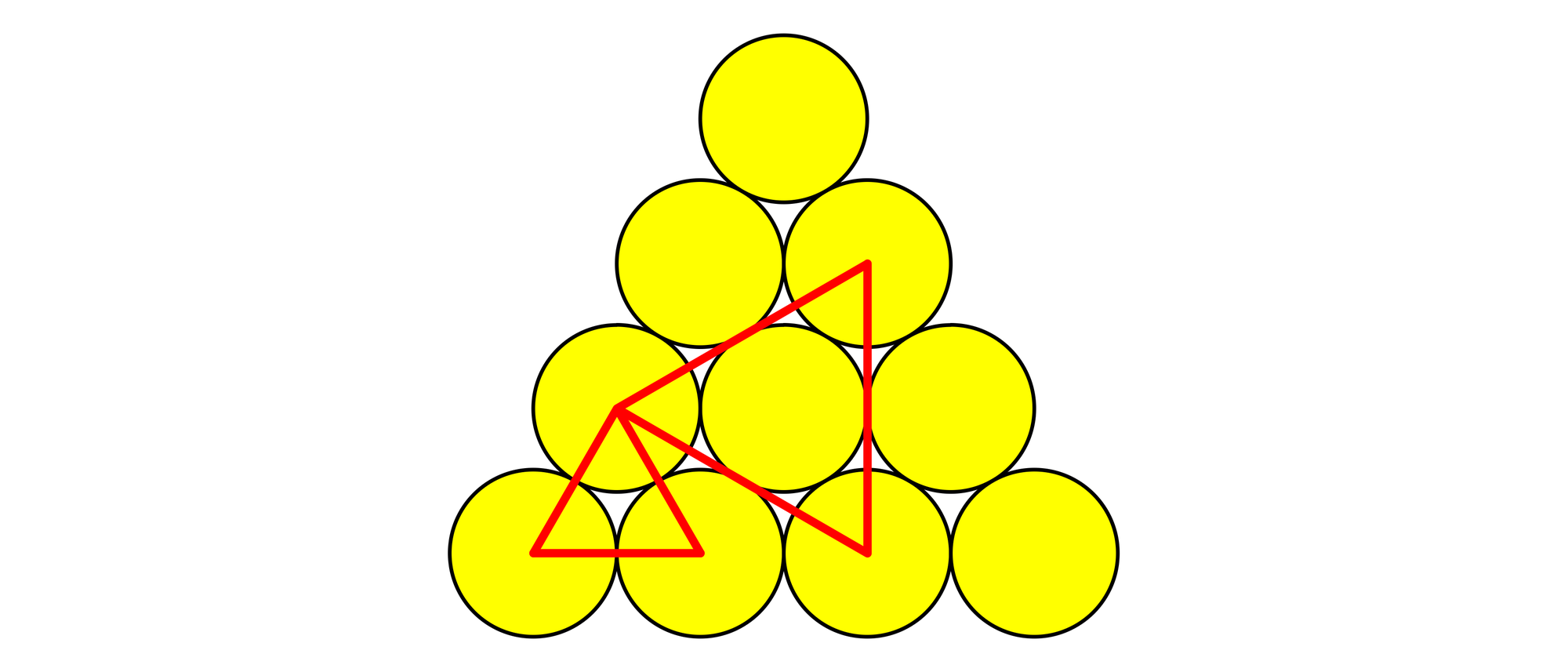
Zehn Ein-Euro-Münzen sind zu einer dreieckigen Figur angeordnet worden. In diese Figur lassen sich nun etliche gleichseitige Dreiecke so einzeichnen, dass jeder ihrer Eckpunkte mit dem Mittelpunkt einer Münze zusammenfällt. In der Skizze sind zwei dieser Dreiecke zu sehen. Wie viele Münzen muss man mindestens aus der Figur entfernen, damit sich kein einziges gleichseitiges Dreieck mehr auf diese Weise einzeichnen lässt?
Es reicht aus, vier Münzen aus der Figur zu entfernen, damit sich kein gleichseitiges Dreieck mehr dort einzeichnen lässt, auf dessen drei Ecken Geldstücke liegen. Diese Lösung ist die einzige, wenn man einmal von Drehungen des Musters absieht, die mit der Fortnahme von vier Münzen auskommt.
Schreiben Sie uns!
Beitrag schreiben